已知a=2015x+2014.b=2015x+2015.c=2015x+2016．求a2+b2+c2-ab-bc-ca的值．题目和参考答案——青夏教育精英家教网—

题目内容

9．已知a=2015x+2014，b=2015x+2015，c=2015x+2016．求a²+b²+c²-ab-bc-ca的值．

分析原式变形后，利用完全平方公式配方后，将已知等式代入计算即可求出值．

解答解：∵a=2015x+2014，b=2015x+2015，c=2015x+2016，
∴a-b=-1，b-c=-1，a-c=-2，
则原式=$\frac{1}{2}$（2a²+2b²+2c²-2ab-2bc-2ac）=$\frac{1}{2}$[（a-b）²+（b-c）²+（a-c）²]=$\frac{1}{2}$×（1+1+4）=3．

点评此题考查了因式分解的应用，熟练掌握完全平方公式是解本题的关键．

练习册系列答案

相关题目

19．三角形内到三边的距离相等的点是（　　）

	A．	三条中线的交点		B．	三条高的交点
	C．	三条角平分线的交点		D．	以上均不对

20．

17．

如图，三个全等的直角三角形正好拼成一个直角△ABC，其中，∠A=90°，那么∠C的度数为30°．

4．已知抛物线y=3（x-2）（x+4），则抛物线的对称轴是x=-1．

14．最大的负整数是-1，绝对值最小的数是0，最小的正整数是1．

1．与多项式3b³-2ab²+4a²b-a³相等的是（　　）

	A．	3b³-（2ab²-4a²b+a³）		B．	3b³-（2ab²+4a²b+a³）
	C．	3b³-（-2ab²+4a²b-a³）		D．	3b³-（2ab²+4a²b-a³）

18．图形在折叠过程中会形成相等的边和相等的角，下面是同学们在数学课上所做的三角形、四边形折叠实验，请根据实验过程解决问题：
问题（一）
如图①，一张三角形ABC纸片，点D、E分别是△ABC边上两点．
研究（1）：如果沿直线DE折叠，使A点落在CE上，则∠BDA′和∠A的数量关系是∠BDA=2∠A；
研究（2）：如果折成图②的形状，猜想∠BDA′、∠CEA′和∠A的数量关系是∠BDA′+∠CEA′=2∠A；
研究（3）：如果折成图③的形状，猜想∠BDA′、∠CEA′和∠A的数量关系，并说明理由．
问题（二）
研究（4）：将问题（一）推广，如图④，将四边形ABCD纸片沿EF折叠，使点A、B落在四边形EFCD的内部时，∠1+∠2与∠A、∠B之间的数量关系是∠1+∠2=2（∠A+∠B）-360°．（直接写出结论）

10．

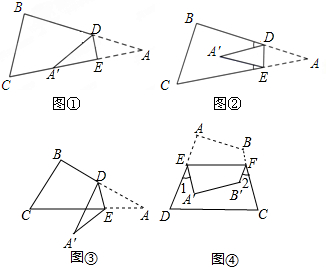
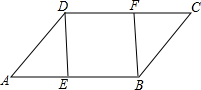如图所示，已知AB=CD，AD=BC，DE=BF，且E，F分别是AB，CD的中点．
（1）求证：∠A=∠C．
（2）求证：∠EDF=∠FBE．

试题分类