Question

12．已知，在三角形ABC中，点D在BC上，DE⊥AB于E，点F在AB上，在CF的延长线上取一点G，连接AG．
（1）如图1，若∠GAB=∠B，∠GAC+∠EDB=180°，求证：AB⊥AC．
（2）如图2．在（1）的条件下，∠GAC的平分线交CG于点M，∠ACB的平分线交AB于点N，当∠AMC-∠ANC=35°时，求∠AGC的度数．

Answer 1

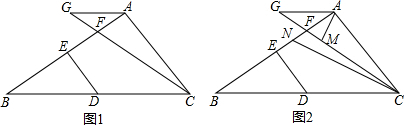
分析 （1）根据平行线的判定和性质可得∠GAC+∠ACB=180°，根据等量关系可得∠EDB=∠ACB，根据平行线的判定和性质可得AB⊥AC．
（2）根据余角的性质可得∠MAB=∠ACN，根据三角形外角的性质、角平分线的性质和平行线的性质可得∠AGC的度数．

解答 解：（1）∵∠GAB=∠B，
∴GA∥BC，
∴∠GAC+∠ACB=180°，
∵∠GAC+∠EDB=180°，
∴∠EDB=∠ACB，
∴ED∥AC，
∵DE⊥AB，
∴AB⊥AC．
（2）∵∠GAC的平分线交CG于点M，∠ACB的平分线交AB于点N，
∴∠ACN+∠MAC=$\frac{1}{2}$×180°=90°，
∵∠MAB+∠MAC=∠ACN+∠MAC=90°，
∴∠MAB=∠ACN=∠NCB，
∵∠AMC-∠ANC=35°，
∴∠BAM+∠NCG=∠BCG=35°，
∵GA∥BC，
∴∠AGC=35°．

点评 本题考查的是三角形的内角和定理，平行线的判定与性质，三角形外角的性质、角平分线的性质掌握三角形内角和等于180°是解题的关键．