题目内容
8.实验与探究:(1)在图1,2,3中,给出平行四边形ABCD的顶点A,B,D的坐标(如图所示),写出图1,2,3中的顶点C的坐标,它们分别是(5,2),(c+e,d),(c+e-a,d);
(2)在图4中,给出平行四边形ABCD的顶点A,B,D的坐标(如图所示),求出顶点C的坐标(C点坐标用含a,b,c,d,e,f的代数式表示);
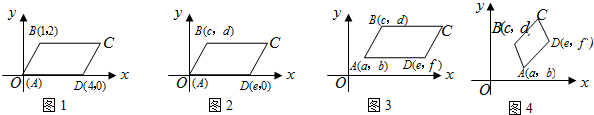
归纳与发现:
(3)通过对图1,2,3,4的观察和顶点C的坐标的探究,你会发现:无论平行四边形ABCD处于直角坐标系中哪个位置,当其顶点坐标为C(如图4)时,则四个顶点的纵坐标b,d,n,f之间的等量关系为b+n=d+f(不必证明);
运用与推广:
(4)在同一直角坐标系中有抛物线y=x2-(5c-3)x-c和三个点$G({-\frac{1}{2}c,\frac{5}{2}c}),S({\frac{1}{2}c,\frac{9}{2}c})$,H(2c,0)(其中c>0).问当c为何值时,该抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形?并求出所有符合条件的P点坐标.
分析 (1)根据对角线的交点是AC的中点,BD的中点,线段中点的性质,可得C点的坐标;
(2)根据对角线的交点是AC的中点,BD的中点,线段中点的性质,可得C点的坐标;
(3)根据线段中点的性质,可得对角线的顶点的纵坐标的和相等;
(4)分类讨论:若GS为平行四边形的对角线,若SH为平行四边形的对角线,若GH为平行四边形的对角线,根据平行四边形对角的顶点坐标的关系,可得P点坐标,根据P点坐标在抛物线上,可得关于c的方程,根据解方程,可得答案.
解答 解:(1)图1,2,3中的顶点C的坐标,它们分别是(5,2),(c+e,d),(c+e-a,d);
(2)顶点C的坐标(C点坐标用含a,b,c,d,e,f的代数式表示):(c+e-a,d+f-b);
(3)四个顶点的纵坐标b,d,n,f之间的等量关系为 b+n=d+f;
故答案为:(c+e-a,d);)(c+e-a,d+f-b);b+n=d+f;
(4)①若GS为平行四边形的对角线,由(3)可得P1(-2c,7c).
要使P1在抛物线上,则有7c=4c2-(5c-3)×(-2c)-c,
即c2-c=0.
∴c1=0(舍去),c2=1.…(1分)
此时P1(-2,7).
②若SH为平行四边形的对角线,由(3)可得P2(3c,2c),
同理可得c=1,此时P2(3,2).
③若GH为平行四边形的对角线,由(3)可得(c,-2c),
同理可得c=1,此时P3(1,-2).
综上所述,当c=1时,抛物线上存在点P,使得以G,S,H,P为顶点的四边形是平行四边形.
符合条件的点有P1(-2,7),P2(3,2),P3(1,-2).
点评 本题考查了二次函数综合题,利用线段中点的性质得出平行四边形对角线上顶点间的关系是解题关键,分类讨论,以防遗漏.

练习册系列答案
相关题目
13.已知菱形的边长为5cm,一条对角线长为8cm,另一条对角线长为( )
| A. | 3cm | B. | 4cm | C. | 6cm | D. | 8cm |
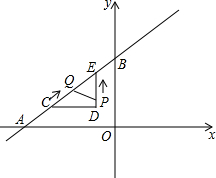 如图,直线y=$\frac{3}{4}$x+6交坐标轴于A、B两点,△CDE与△AOB形状完全相同,已知∠D=90°,CD=4,Q为△CDE斜边上的中点.点C从点A出发,以每秒5个单位长度的速度带动整个△CDE沿射线AB方向平移,同时,点P从顶点D出发,以每秒1个单位长度的速度沿直角边DE运动,当点P到达点E时,点P停止运动,△CDE也随之停止平移.设运动时间为t秒.
如图,直线y=$\frac{3}{4}$x+6交坐标轴于A、B两点,△CDE与△AOB形状完全相同,已知∠D=90°,CD=4,Q为△CDE斜边上的中点.点C从点A出发,以每秒5个单位长度的速度带动整个△CDE沿射线AB方向平移,同时,点P从顶点D出发,以每秒1个单位长度的速度沿直角边DE运动,当点P到达点E时,点P停止运动,△CDE也随之停止平移.设运动时间为t秒.