题目内容
17.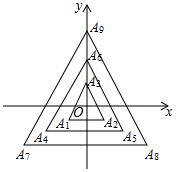 如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )
如图,△A1A2A3,△A4A5A6,△A7A8A9…,△A3n-2A3n-1A3n(n为正整数)均为等边三角形,它们的边长依次为2,4,6,…,2n,顶点A3,A6,A9…A3n均在y轴上,点O是所有等边三角形的中心,则点 A2016 的坐标为( )| A. | (0,448) | B. | (-672,$224\sqrt{3}$) | C. | (0,$448\sqrt{3}$) | D. | (0,$224\sqrt{3}$) |
分析 先关键等边三角形的性质和已知条件得出A3的坐标,根据每一个三角形有三个顶点确定出A2016所在的三角形,再求出相应的三角形的边长以及A2016的纵坐标的长度,即可得解.
解答 解:∵△A1A2A3为等边三角形,边长为2,点A3,A6,A9,…,A3n均在y轴上,点O是所有等边三角形的中心,
∴A3的坐标为(0,$\frac{2\sqrt{3}}{3}$),
∵2016÷3=672,
∴A2016是第672个等边三角形的第3个顶点,
∴点A2016的坐标为(0,$\frac{2}{3}$×$\frac{1344}{2}$$\sqrt{3}$),
即点A2016的坐标为(0,448$\sqrt{3}$);
故选:C.
点评 本题是点的变化规律的考查,主要利用了等边三角形的性质,确定出点A3和A2016所在三角形是解题的关键.

练习册系列答案
相关题目
8.十边形的内角和为( )
| A. | 1800° | B. | 1620° | C. | 1440° | D. | 1260° |
12.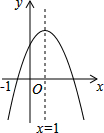 已知二次函数的图象如图,则下列结论中正确的有( )
已知二次函数的图象如图,则下列结论中正确的有( )
①a+b+c>0;②a-b+c<0;③b>0;④b=2a;⑤abc<0.
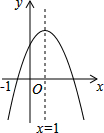 已知二次函数的图象如图,则下列结论中正确的有( )
已知二次函数的图象如图,则下列结论中正确的有( )①a+b+c>0;②a-b+c<0;③b>0;④b=2a;⑤abc<0.
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
2.若a=-22,b=(-2)-2,c=(-$\frac{1}{2}$)-2,d=(-$\frac{1}{2}$)0,则a,b,c,d的大小关系是( )
| A. | b<d<c<a | B. | a<b<d<c | C. | b<a<d<c | D. | a<d<b<c |
9.对于数据:1,7,5,5,3,4,3.下列说法中错误的是( )
| A. | 这组数据的平均数是4 | B. | 这组数据的众数是5和3 | ||
| C. | 这组数据的中位数是4 | D. | 这组数据的方差是22 |
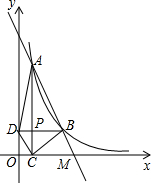 如图,直线AB经过x轴上的点M,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.
如图,直线AB经过x轴上的点M,与反比例函数y=$\frac{k}{x}$(x>0)的图象相交于点A(1,8)和B(m,n),其中m>1,AC⊥x轴于点C,BD⊥y轴于点D,AC与BD交于点P.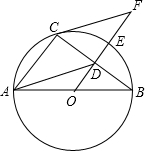 如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.
如图,AB是半圆O的直径,D为BC的中点,延长OD交弧BC于点E,点F为OD的延长线上一点且满足∠OBC=∠OFC.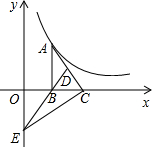 如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )
如图,Rt△ABC的边BC在x轴正半轴上,点D为AC的中点,DB的延长线交y轴负半轴于点E,反比例函数y=$\frac{k}{x}$(x>0)的图象经过点A,若S△BEC=6,则k的值为( )