题目内容
7.在△ABC中,AB=AC,若BD⊥AC于D,若cos∠BAD=$\frac{2}{3}$,BD=$\sqrt{5}$,则CD为1或5.分析 分△ABC为锐角三角形和钝角三角形两种情况,在Rt△ABD中由cos∠BAD=$\frac{AD}{AB}$=$\frac{2}{3}$,可设设AD=2x,则AB=3x,结合BD的长根据勾股定理可得$9{x}^{2}=4{x}^{2}+(\sqrt{5})^{2}$,求得x的值后即可得AB=AC=3,AD=2,在锐角三角形中CD=AC-AD,在钝角三角形中CD=AC+AD即可得答案.
解答 解:①如图1,若△ABC为锐角三角形,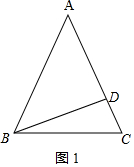
∵BD⊥AC,
∴∠ADB=90°,
∵cos∠BAD=$\frac{AD}{AB}$=$\frac{2}{3}$,
∴设AD=2x,则AB=3x,
∵AB2=AD2+BD2,
∴$9{x}^{2}=4{x}^{2}+(\sqrt{5})^{2}$,
解得:x=1或x=-1(舍),
∴AB=AC=3x=3,AD=2x=2,
∴CD=AC-AD=1;
②如图2,若△ABC为钝角三角形,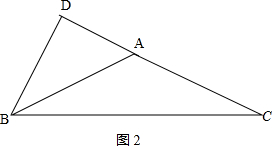
由①知,AD=2x=2,AB=AC=3x=3,
∴CD=AC+AD=5,
故答案为:1或5.
点评 本题考查了等腰三角形的性质,解直角三角形,勾股定理的应用,解此题的关键是根据三角形的形状分类讨论.

练习册系列答案
相关题目
2. 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
 如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )
如图,一棵9m高的树被风折断,树顶落在离树根3m之处,若要查看断痕,要从树底开始爬多高?( )| A. | 2.5m | B. | 3m | C. | 3.5m | D. | 4m |
19.将正偶数按表格方式排成5列若干行:
根据上述规律,数2016应在( )
| 第1列 | 第2列 | 第3列 | 第4列 | 第5列 | |
| 第1行 | 2 | 4 | 6 | 8 | |
| 第2行 | 16 | 14 | 12 | 10 | |
| 第3行 | 18 | 20 | 22 | 24 | |
| 第4行 | 32 | 30 | 28 | 26 | |
| … | … | … | … | … | … |
| A. | 第251行 第1列 | B. | 第251行 第5列 | C. | 第252行 第4列 | D. | 第252行 第1列 |
16.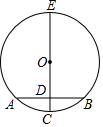 如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
①AD=BD;②$\widehat{AC}$=$\widehat{BC}$;③$\widehat{AE}$=$\widehat{BE}$;④OD=CD.
 如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )
如图,CE是圆O的直径,⊙O的直径,AB为⊙O的弦,EC⊥AB,垂足为D,下面结论正确的有( )①AD=BD;②$\widehat{AC}$=$\widehat{BC}$;③$\widehat{AE}$=$\widehat{BE}$;④OD=CD.
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
17.在一次函数y=(m+1)x+5中,y随x的增大而减小,则m的取值范围是( )
| A. | m<-1 | B. | m>-1 | C. | m=-1 | D. | m<1 |
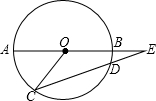 如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数.
如图,A、B、C、D均为⊙O上的点,其中A、B两点的连线经过圆心O,线段AB、CD的延长线交于点E,已知AB=2DE,∠E=18°,求∠AOC的度数. 如图是一个数值转换器,当输入-1时,请计算出输出结果?(要有计算过程)
如图是一个数值转换器,当输入-1时,请计算出输出结果?(要有计算过程)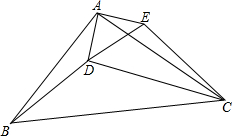 如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由.
如图,△ABC中,AB=AC,点D在△ABC内部,以AD为腰作等腰△ADE,AD=AE,且∠BAC=∠DAE=100°,∠BDC=140°,∠BDA=α,连接BD、CD,当α=130°时,试判断△CDE的形状,并说明理由.