题目内容
19.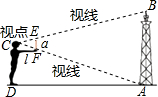 如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45cm,小尺长a=15cm,点D到铁塔底部的距离AD=42m,则铁塔的高度是14m.
如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45cm,小尺长a=15cm,点D到铁塔底部的距离AD=42m,则铁塔的高度是14m.
分析 作CH⊥AB于H,交EF于P,如图,则CH=DA=42m,CP=45cm=0.45m,EF=15cm=0.15m,证明△CEF∽△CBA,然后利用相似比计算出AB即可.
解答 解:作CH⊥AB于H,交EF于P,如图,则CH=DA=42m,CP=45cm=0.45m,EF=15cm=0.15m,
∵EF∥AB,
∴△CEF∽△CBA,
∴$\frac{EF}{AB}$=$\frac{CP}{CH}$,即$\frac{0.15}{AB}$=$\frac{0.45}{42}$,
∴AB=14(m),
即铁塔的高度为14m.
故答案为14.
点评 本题考查了相似三角形的应用:利用杆或直尺测量物体的高度就是利用杆或直尺的高(长)作为三角形的边,利用视点和盲区的知识构建相似三角形,用相似三角形对应边的比相等的性质求物体的高度.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
14.已知关于x的方程$\frac{m-1}{x-1}=\frac{x}{x-1}$=0的解为非负数,则m的取值范围是( )
| A. | m≥1 | B. | m≥1且m≠2 | C. | m≤1且m≠2 | D. | m≤1 |
11.某公司为一种新型电子产品在该城市的特约经销商,已知每件产品的进价为40元,该公司每年销售这种产品的其他开支(不含进货价)总计100万元,在销售过程中得知,年销售量y(万件)与销售单价x(元)之间存在如表所示的函数关系,并且发现y是x的一次函数.
(1)求y与x的函数关系式;
(2)当销售单价x为何值时,该公司年利润为75万元?[备注:年利润=年销售额-总进货价-其他开支].
| 销售单价x(元) | 50 | 60 | 70 | 80 |
| 销售数量y(万件) | 5.5 | 5 | 4.5 | 4 |
(2)当销售单价x为何值时,该公司年利润为75万元?[备注:年利润=年销售额-总进货价-其他开支].
 如图,将一块实心三角板和实心半圆形量角器按图中方式叠放,三角板一直角边与量角器的零刻度线所在直线重合,斜边与半圆相切,重叠部分的量角器弧对应的圆心角(∠AOB)为120°,BC的长为2$\sqrt{3}$,则三角板和量角器重叠部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$.
如图,将一块实心三角板和实心半圆形量角器按图中方式叠放,三角板一直角边与量角器的零刻度线所在直线重合,斜边与半圆相切,重叠部分的量角器弧对应的圆心角(∠AOB)为120°,BC的长为2$\sqrt{3}$,则三角板和量角器重叠部分的面积为$\frac{16π}{3}$+2$\sqrt{3}$. 如图,某小区有一块长为24米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为72米2,两块绿地之间及周边留有宽度相等的人行通道.求人行道的宽度.
如图,某小区有一块长为24米,宽为8米的矩形空地,计划在其中修建两块相同的矩形绿地,它们的面积之和为72米2,两块绿地之间及周边留有宽度相等的人行通道.求人行道的宽度.