题目内容
9.如果方程(x-2)(x-3)=0的两个根分别是Rt△ABC的两条直角边,△ABC最小的角的顶点为A,那么tanA的值为$\frac{2}{3}$.分析 利用因式分解法求出Rt△ABC的两条直角边的长,再解直角三角形即可.
解答 解:∵(x-2)(x-3)=0,
∴x-2=0,x-3=0,
∴x1=2,x2=3,
∵△ABC最小的角的顶点为A,
∴tanA=$\frac{2}{3}$.
故答案为:$\frac{2}{3}$.
点评 本题主要考查了因式分解法解一元二次方程以及锐角三角函数的定义,解答本题的关键利用因式分解法求出两边的长,此题难度不大.

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
20. 如图,△ABC的三个顶点分别在正方形网格的格点上,则tanC的值是( )
如图,△ABC的三个顶点分别在正方形网格的格点上,则tanC的值是( )
 如图,△ABC的三个顶点分别在正方形网格的格点上,则tanC的值是( )
如图,△ABC的三个顶点分别在正方形网格的格点上,则tanC的值是( )| A. | $\frac{6}{5}$ | B. | $\frac{2\sqrt{10}}{3}$ | C. | $\frac{5}{6}$ | D. | $\frac{3\sqrt{10}}{3}$ |
4.每天你是如何醒来的?某校有4000名学生,从不同班级不同层次抽取了400名学生进行调查,下表是这400名学生早晨起床方式的统计表:
回答下列问题:
(1)该问题中总体是某校4000名学生早晨起床的情况;
(2)样本是400名学生早晨起床的情况;样本的容量是400;
(3)个体是每一名学生早晨起床的情况;
(4)估计全校学生中自己醒来的人数为640人.
| 起床方式 | 人数 |
| 别人叫醒 | 172 |
| 闹钟 | 88 |
| 自己醒来 | 64 |
| 其它 | 76 |
(1)该问题中总体是某校4000名学生早晨起床的情况;
(2)样本是400名学生早晨起床的情况;样本的容量是400;
(3)个体是每一名学生早晨起床的情况;
(4)估计全校学生中自己醒来的人数为640人.
14.在Rt△ABC中,∠C=90°,∠A、∠B、∠C的对边分别是a、b、c,则下列关系中错误的是( )
| A. | a=btanB | B. | a=ccosB | C. | b=csinB | D. | a=btanA |
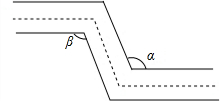 如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是,理由是内错角相等,两直线平行.
如图,是一条暖气管道的剖面图,如果要求管道拐弯前后的方向保持不变,那么管道的两个拐角∠α与∠β之间应该满足的关系是,理由是内错角相等,两直线平行.
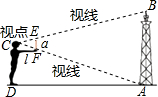 如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45cm,小尺长a=15cm,点D到铁塔底部的距离AD=42m,则铁塔的高度是14m.
如图,小明把手臂水平向前伸直,手持小尺竖直,瞄准小尺的两端E、F,不断调整站立的位置,使在点D处恰好能看到铁塔的顶部B和底部A,设小明的手臂长l=45cm,小尺长a=15cm,点D到铁塔底部的距离AD=42m,则铁塔的高度是14m.