题目内容
18．现有点数为2，3，4，5的四张扑克牌背面朝上，洗匀后，从中任意抽出两张牌，这两张牌上的数字之和能被3整除的概率是$\frac{1}{3}$．分析 先画出树状图展示所有12种等可能的结果数，再找出这两张牌上的数字之和能被3整除的结果数，然后根据概率公式求解．
解答 解：画树状图为：
共有12种等可能的结果数，其中这两张牌上的数字之和能被3整除的结果数有4种，
所以这两张牌上的数字之和能被3整除的概率=$\frac{4}{12}$=$\frac{1}{3}$．
故答案为$\frac{1}{3}$．
点评 本题考查了列表法或树状图法：通过列表法或树状图法展示所有等可能的结果求出n，再从中选出符合事件A或B的结果数目m，然后根据概率公式求出事件A或B的概率．
练习册系列答案
轻巧夺冠周测月考直通中考系列答案
相关题目
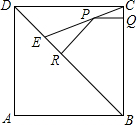如图，E是边长为1的正方形ABCD的对角线BD上的一点，且BE=BA，P是CE上任意一点，PQ⊥BC于点Q，PR⊥BE于点R．则：（1）DE=$\sqrt{2}$-1；（2）PQ+PR=$\frac{\sqrt{2}}{2}$．
13．
如图是正方形的展开图，原正方体相对两个面上的数字之和的最小值是（ ）
如图是正方形的展开图，原正方体相对两个面上的数字之和的最小值是（ ）| A． | 4 | B． | 5 | C． | 6 | D． | 7 |
5．两个边长分别为1，2，$\sqrt{5}$的三角形，拼成一个四边形，则能拼成几种不同的四边形．（ ）
| A． | 2种 | B． | 3种 | C． | 4种 | D． | 5种 |