题目内容
18.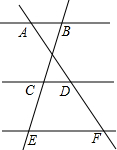 如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长是$\frac{24}{5}$.
如图,已知AB∥CD∥EF,AD:AF=3:5,BE=12,那么CE的长是$\frac{24}{5}$.
分析 由AB∥CD∥EF,可知$\frac{AD}{AF}=\frac{CB}{BE}$,从而可求得BC=$\frac{36}{5}$,最后根据CE=BE-BC求解即可.
解答 解:∵AB∥CD∥EF,
∴$\frac{AD}{AF}=\frac{CB}{BE}$,即$\frac{3}{5}=\frac{CB}{12}$.
∴BC=$\frac{36}{5}$.
CE=BE-BC=12-$\frac{36}{5}$=$\frac{24}{5}$.
故答案为:$\frac{24}{5}$.
点评 本题主要考查的是平行线分线段成比例定理的应用,根据定理列出比例式求得BC的长度是解题的关键.

练习册系列答案
相关题目
13. 如图是正方形的展开图,原正方体相对两个面上的数字之和的最小值是( )
如图是正方形的展开图,原正方体相对两个面上的数字之和的最小值是( )
 如图是正方形的展开图,原正方体相对两个面上的数字之和的最小值是( )
如图是正方形的展开图,原正方体相对两个面上的数字之和的最小值是( )| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
9.x=2是3x+2a=4的解,则a的值为( )
| A. | -1 | B. | 1 | C. | -5 | D. | 5 |
13.学校开展为贫困地区捐书活动,以下是5名同学捐书的册数:2,3,x,3,8.已知这组数据的平均数是4,则这组数据的中位数和众数分别是( )
| A. | 3和4 | B. | 3和3 | C. | 4和3 | D. | 3和2 |
7. 如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )
如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )
 如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )
如图,已知△ABC为等边三角形,若沿图中虚线剪去∠B,则∠1+∠2等于( )| A. | 120° | B. | 135° | C. | 240° | D. | 315° |
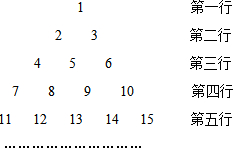 如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.
如下数表是由从1开始的连续自然数组成,观察规律并完成各题的解答.