题目内容
6.在平面直角坐标系xOy中,点P(4,a)在正比例函数y=$\frac{1}{2}$x的图象上,则点Q(2a-5,a)关于y轴的对称点Q'坐标为(1,2).分析 把点P坐标代入正比例函数解析式可得a的值,进而求得Q点的坐标,然后根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可直接得到答案.
解答 解:∵点P(4,a)在正比例函数y=$\frac{1}{2}$x的图象上,
∴a=2,
∴2a-5=-1,
∴Q(-1,2),
∴点Q(-1,2)关于y轴的对称点Q′的坐标为(1,2),
故答案为:(1,2).
点评 本题考查了一次函数图象上点的坐标特征以及关于y轴对称点的坐标特点,得到a的值是解决本题的突破点.

练习册系列答案
相关题目
1.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( )
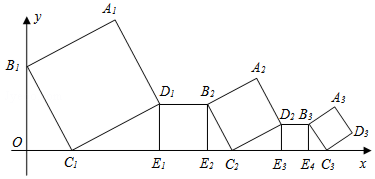

| A. | ($\frac{1}{2}$)2016 | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2017 |
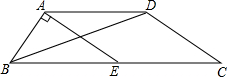 如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,点E是BC的中点,连接AE,BD,若EA⊥AB,BC=26,DC=12,求△ABD的面积.
如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,点E是BC的中点,连接AE,BD,若EA⊥AB,BC=26,DC=12,求△ABD的面积. 小明爸爸骑着摩托车带着小明以每小时60千米的速度在公路上匀速行驶,如图是小明在上午8:00和10:00看的路边的里程碑的里程情况.
小明爸爸骑着摩托车带着小明以每小时60千米的速度在公路上匀速行驶,如图是小明在上午8:00和10:00看的路边的里程碑的里程情况.