题目内容
1.一组正方形按如图所示的方式放置,其中顶点B1在y轴上,顶点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…,则正方形A2017B2017C2017D2017的边长是( )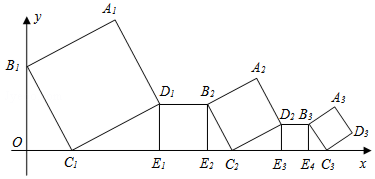
| A. | ($\frac{1}{2}$)2016 | B. | ($\frac{1}{2}$)2017 | C. | ($\frac{\sqrt{3}}{3}$)2016 | D. | ($\frac{\sqrt{3}}{3}$)2017 |
分析 利用正方形的性质结合锐角三角函数关系得出正方形的边长,进而得出变化规律即可得出答案.
解答 解:∵正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3,
∴D1E1=B2E2,D2E3=B3E4,∠D1C1E1=∠C2B2E2=∠C3B3E4=30°,
∴D1E1=C1D1sin30°=$\frac{1}{2}$,
则B2C2=$\frac{{B}_{2}{E}_{2}}{cos30°}$=$\frac{\sqrt{3}}{3}$=( $\frac{\sqrt{3}}{3}$)1,
同理可得:B3C3=$\frac{1}{3}$=( $\frac{\sqrt{3}}{3}$)2,
故正方形AnBnCnDn的边长是:( $\frac{\sqrt{3}}{3}$)n-1,
则正方形A2017B2017C2017D2017的边长为:( $\frac{\sqrt{3}}{3}$)2016,
故选:C.
点评 此题主要考查了正方形的性质以及锐角三角函数等知识,得出正方形的边长变化规律是解题关键.

练习册系列答案
相关题目
12.阅读可以增进人们的知识也能陶冶人们的情操.我们要多阅读,多阅读有营养的书.因此我校对学生的课外阅读时间进行了抽样调查,将收集的数据分成A、B、C、D、E五组进行整理,并绘制成如图所示的统计图表(图中信息不完整).
请结合以上信息解答下列问题
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.
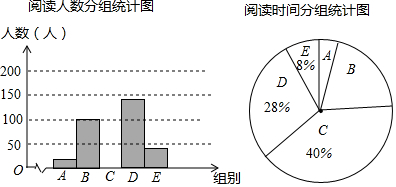
| 阅读时间分组统计表 | ||
| 组别 | 阅读时间x(h) | 人数 |
| A | 0≤x<10 | a |
| B | 10≤x<20 | 100 |
| C | 20≤x<30 | b |
| D | 30≤x<40 | 140 |
| E | x≥40 | c |
(1)求a,b,c的值;
(2)补全“阅读人数分组统计图”;
(3)估计全校课外阅读时间在20h以下(不含20h)的学生所占百分比.

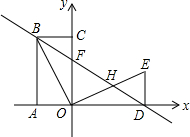 如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.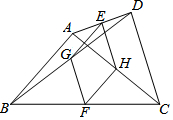 如图,在四边形ABCD中,AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,顺次连接E、G、F、H.
如图,在四边形ABCD中,AB=CD,E、F、G、H分别为AD、BC、BD、AC的中点,顺次连接E、G、F、H.