题目内容
11.三元一次方程组$\left\{\begin{array}{l}{x+y-z=3}\\{x+y+z=1}\\{-x+2y+z=3}\end{array}\right.$的解为$\left\{\begin{array}{l}{x=0}\\{y=2}\\{z=-1}\end{array}\right.$.分析 方程组利用加减消元法求出解即可.
解答 解:$\left\{\begin{array}{l}{x+y-z=3①}\\{x+y+z=1②}\\{-x+2y+z=3③}\end{array}\right.$,
①+②得:x+y=2④,
①+③得:3y=6,
解得:y=2,
把y=2代入④得:x=0,
把x=0,y=2代入①得:z=-1,
则方程组的解为$\left\{\begin{array}{l}{x=0}\\{y=2}\\{z=-1}\end{array}\right.$.
故答案为:$\left\{\begin{array}{l}{x=0}\\{y=2}\\{z=-1}\end{array}\right.$
点评 此题考查了解三元一次方程组,利用了消元的思想,消元的方法有:代入消元法与加减消元法.

练习册系列答案
 考前必练系列答案
考前必练系列答案
相关题目
19.把多项式m2-9m分解因式,结果正确的是( )
| A. | m(m-9) | B. | (m+3)(m-3) | C. | m(m+3)(m-3) | D. | (m-3)2 |
20.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明( )


| A. | 三角形任意两边之和大于第三边 | B. | 三角形任意两边之差小于第三边 | ||
| C. | 三角形外角和等于360° | D. | 三角形内角和等于180° |
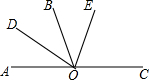 如图,O为直线AC上一点,OD是∠AOB的平分线,OE在∠BOC的内部,∠BOE=36°,∠EOC=$\frac{2}{3}$∠BOC.求∠AOD的度数.
如图,O为直线AC上一点,OD是∠AOB的平分线,OE在∠BOC的内部,∠BOE=36°,∠EOC=$\frac{2}{3}$∠BOC.求∠AOD的度数.