题目内容
16.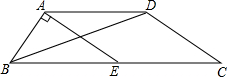 如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,点E是BC的中点,连接AE,BD,若EA⊥AB,BC=26,DC=12,求△ABD的面积.
如图,在四边形ABCD中,AD∥BC,AD=$\frac{1}{2}$BC,点E是BC的中点,连接AE,BD,若EA⊥AB,BC=26,DC=12,求△ABD的面积.
分析 连接DE,根据点E是BC的中点,AD=$\frac{1}{2}$BC可得出四边形ABED与四边形AECD都是平行四边形,故可得出AE=DC=12,S△ABD=$\frac{1}{2}$S?ABED,根据勾股定理求出AB的长,进而可得出结论.
解答 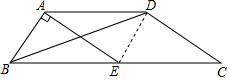 解:连接DE,
解:连接DE,
∵点E是BC的中点,BC=26,
∴BE=EC=$\frac{1}{2}$BC=13,
∵AD=$\frac{1}{2}$BC,
∴AD=BE=CE=13.
∵AD∥BE,
∴四边形ABED与四边形AECD都是平行四边形,
∴AE=DC=12,S△ABD=$\frac{1}{2}$S?ABED.
在△ABE中,
∵∠BAE=90°,
∴AB=$\sqrt{B{E}^{2}-A{E}^{2}}$=$\sqrt{1{3}^{2}-1{2}^{2}}$=5,
∴S△ABD=$\frac{1}{2}$S?ABED=$\frac{1}{2}$×5×12=30.
点评 本题考查的是平行四边形的判定与性质,根据题意作出辅助线,构造出平行四边形是解答此题的关键.

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
14.若-2amb4与5an+2b2m+n是同类项,则mn的值是( )
| A. | 2 | B. | 0 | C. | -1 | D. | 1 |
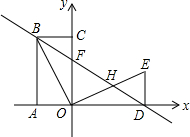 如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H.
如图,四边形OABC是矩形,点A、C在坐标轴上,B点坐标(-2,4)△ODE是△OCB绕点O顺时针旋转90°得到的,点D在x轴上,直线BD交y轴于点F,交OE于点H. 定义新运算:对于任意实数a,b都有a⊕b=a(a+b)-2,等式右边是通常的加法、减法及乘法运算,比如:3⊕8=3×(3+8)-2=3×11-2=33-2=31
定义新运算:对于任意实数a,b都有a⊕b=a(a+b)-2,等式右边是通常的加法、减法及乘法运算,比如:3⊕8=3×(3+8)-2=3×11-2=33-2=31