题目内容
2.已知四边形ABCD各顶点坐标分别为A(3,-2),B(3,2),C(-3,2),D(-3,-2).(1)建立平面直角坐标系,并画出四边形ABCD.
(2)求四边形ABCD的面积.
分析 (1)建立平面直角坐标系,然后找出A、B、C、D各点的位置即可;
(2)根据四边形ABCD为矩形,即可解答.
解答 解:(1)如图所示:
(2)由图象可知:四边形ABCD为矩形,
∵A(3,-2),B(3,2),C(-3,2),D(-3,-2),
∴AB=4,AD=6,
∴四边形ABCD的面积为:4×6=24.
点评 本题考查了坐标与图形性质,解决本题的关键是利用了平面直角坐标系与点的关系.

练习册系列答案
 寒假学与练系列答案
寒假学与练系列答案
相关题目
12.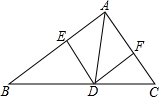 如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
 如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
17.实数-2,0.3,$\frac{1}{7}$,$\sqrt{2}$,-π中,无理数的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
14.在平面直角坐标系中,如果点A的坐标为(m2+1,-2015),那么点A在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
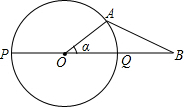 如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论:
如图,PQ为⊙O的直径,点B在线段PQ的延长线上,OQ=QB=1,动点A在⊙O的上半圆运动(含P、Q两点),连结AB,设∠AOB=α.有以下结论: 如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°.
如图,把一块直角三角板的直角顶点放在直尺的一边上,如果∠1=15°,那么∠2的度数是75°. 如图,三条直线交于同一点,则∠1+∠2+∠3=180°.
如图,三条直线交于同一点,则∠1+∠2+∠3=180°.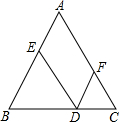 如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.
如图,在等边△ABC的底边BC边上任取一点D,过点D作DE∥AC交AB于点E,作DF∥AC交AC于点F,DE=5cm,DF=3cm,则△ABC的周长为24cm.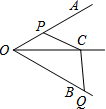 如图,∠AOB=60°,点C在∠AOB的平分线上,OC=4,点P、Q分别是射线OA、OB上不同于O的一点,且四边形OPCQ的内角∠PCQ=120°.设CP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )
如图,∠AOB=60°,点C在∠AOB的平分线上,OC=4,点P、Q分别是射线OA、OB上不同于O的一点,且四边形OPCQ的内角∠PCQ=120°.设CP=x,CQ=y,则下列图象中,能表示y与x的函数关系的图象大致是( )