题目内容
12.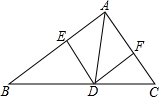 如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )
如图,在△ABC中,DE∥CA,DF∥BA,下列四个判断不正确的是( )| A. | 四边形AEDF是平行四边形 | |
| B. | 如果∠BAC=90°,那么四边形AEDF是矩形 | |
| C. | 如果AD平分∠BAC,那么四边形AEDF是矩形 | |
| D. | 如果AD⊥BC,且AB=AC,那么四边形AEDF是菱形 |
分析 由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形;
如果AD⊥BC且AB=AC,那么AD平分∠BAC,同上可得四边形AEDF是菱形.
故以上答案都正确.
解答 解:由DE∥CA,DF∥BA,根据两组对边分别平行的四边形是平行四边形可得四边形AEDF是平行四边形;
又有∠BAC=90°,根据有一角是直角的平行四边形是矩形,可得四边形AEDF是矩形.故A、B正确;
如果AD平分∠BAC,那么∠EAD=∠FAD,又有DF∥BA,可得∠EAD=∠ADF,
∴∠FAD=∠ADF,
∴AF=FD,那么根据邻边相等的平行四边形是菱形,可得四边形AEDF是菱形,而不一定是矩形.故C错误;
如果AD⊥BC且AB=AC,那么AD平分∠BAC,同上可得四边形AEDF是菱形.故D正确.
故选C.
点评 本题考查平行四边形、矩形及菱形的判定,具体选择哪种方法需要根据已知条件来确定.

练习册系列答案
相关题目
3.下列说法中,正确的有( )
(1)$\sqrt{25}$的平方根是±5;
(2)五边形的内角和是540°.
(3)抛物线y=x2+2x+4与x轴无交点.
(4)等腰三角形两边长为6cm和4cm,则它的周长是16cm.
(1)$\sqrt{25}$的平方根是±5;
(2)五边形的内角和是540°.
(3)抛物线y=x2+2x+4与x轴无交点.
(4)等腰三角形两边长为6cm和4cm,则它的周长是16cm.
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 5个 |
20.用一副三角板的内角可以画出大于0°且小于180°的不同角度的角共有( )
| A. | 9种 | B. | 10种 | C. | 11种 | D. | 12种 |
17.下列每组数分别是三根小木棒的长度,用它们能摆成三角形的是( )
①7cm,5cm,11cm ②4cm,3cm,7cm ③5cm,10cm,4cm ④2cm,3cm,1cm.
①7cm,5cm,11cm ②4cm,3cm,7cm ③5cm,10cm,4cm ④2cm,3cm,1cm.
| A. | ① | B. | ② | C. | ③ | D. | ④ |
1.下列各式中,正确的是( )
| A. | $\frac{6-2x}{-x+3}$=2 | B. | $\frac{a-b}{(a-b)(a+b)}$=0 | C. | $\frac{(a-b)^{3}}{(b-a)^{3}}$=1 | D. | $\frac{(a-b)^{2}}{(b-a)^{2}}$=-1 |
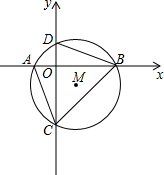 如图,在直角坐标系中,半径为$\sqrt{5}$,圆心为M的⊙M经过A,B,C三点,已知点M的纵坐标为-1,点C的坐标为(0,3),OA:OB=1:3,⊙M与y轴交于点D
如图,在直角坐标系中,半径为$\sqrt{5}$,圆心为M的⊙M经过A,B,C三点,已知点M的纵坐标为-1,点C的坐标为(0,3),OA:OB=1:3,⊙M与y轴交于点D