题目内容
5.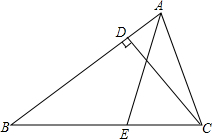 如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数.
如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数.
分析 先根据CD为△ABC的高,求∠BDC的度数,再结合图形根据角的和差求出∠ACD的度数,利用三角形的内角和求∠BAC,因AE为△ABC的角平分线,所以可得∠CAE,最后利用△AFC的内角和为180°,求得∠AFC的度数.
解答 解:∵CD为△ABC的高,
∴∠BDC=90°,
∵∠B=30°,
∴∠BCD=60°,
又∵∠ACB=75°,
∴∠ACD=∠ACB-∠BCD=15°,
∴∠BAC=180°-∠B-∠ACB=75°,
∵AE为△ABC的角平分线,
∴∠CAE=$\frac{1}{2}$∠BAC=37.5°,
∴∠AFC=180°-∠CAE-∠ACD=127.5°.
点评 此题考查三角形的角平分线、高的意义,三角形的内角和定理,结合图形,理解题意,灵活运用定义域定理解决问题.

练习册系列答案
相关题目
16. 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )
 如图是某几何体的三视图,该几何体是( )
如图是某几何体的三视图,该几何体是( )| A. | 圆锥 | B. | 三棱柱 | C. | 圆柱 | D. | 三棱锥 |
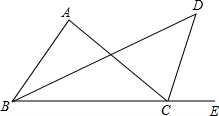 如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数.
如图,△ABC中,∠A=90°,∠ABC的平分线与∠ACE的平分线相交于点D,求∠D的度数. 如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=125°,求∠DFB和∠DGB的度数.
如图,已知△ABC≌△ADE,且∠CAD=10°,∠B=∠D=25°,∠EAB=125°,求∠DFB和∠DGB的度数. 如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).
如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).