题目内容
10. 如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).
如图,平面直角坐标系中,O是坐标原点,抛物线C1:y=ax2经过点(1,-1).(1)求抛物线C1的解析式;
(2)将抛物线C1平移后得到抛物线C2,若抛物线C2经过点(0,2),且对称轴为直线x=1,请你说明:将抛物线C1如何平移可得到抛物线C2;
(3)将(2)中得到的抛物线C2沿其对称轴向下平移,得到抛物线C3,设抛物线C3的顶点为A,直线OA与抛物线C3的另一个交点为B,对称轴与x轴的交点为P,当OP=AP时.求点A的坐标及∠ABP的正弦值.
分析 (1)把点(1,-1)代入抛物线解析式,列出关于系数a的方程,通过方程来求a的值;
(2)利用待定系数法求得平移后抛物线的解析式,易求平移后的抛物线的顶点坐标,根据抛物线平移前后顶点坐标的变化来推断抛物线的平移规律;
(3)需要对点A的位置进行分类讨论:点A在x轴的上方和点A在x轴的下方两种情况.根据点A的坐标易求直线OA的解析式,由直线OA和抛物线C3的交点来求点B的坐标即可.
解答  解:(1)把(1,-1)代入y=ax2,
解:(1)把(1,-1)代入y=ax2,
得a=-1,
故该抛物线的解析式为:y=-x2;
(2)抛物线C2是由抛物线C1向右平移1个单位,向上平移3个单位得到的.理由如下:
设抛物线C2的解析式为:y=-(x-1)2+k.
把(0,2)代入,
得 2=-1+k,
解得k=3.
故抛物线C2的解析式为:y=-(x-1)2+3,
则其顶点坐标为(1,3).
所以由抛物线C1的顶点(0,0)向右平移1个单位,再向上平移3个单位得到抛物线C2的顶点坐标(1,3).
所以,抛物线C2是由抛物线C1向右平移1个单位,向上平移3个单位得到的.
(3)当OP=AP时,A(1,1)或(1,-1).
当A(1,1)时,y=-(x-1)2+1,直线OA与抛物线没有交点B.
故A(1,-1).
所以抛物线C3的解析式为:y=-(x-1)2-1.
∴直线OA是二、四象限的角平分线,设B(a,-a),a>0,
则-a=-(a-1)2-1,
解得a1=1(舍去),a2=2,
∴B(2,-2).
设P点到OA的距离是h,则h=$\frac{\sqrt{2}}{2}$×1=$\frac{\sqrt{2}}{2}$,
∴PB=$\sqrt{{1}^{2}+{2}^{2}}$=$\sqrt{5}$,
∴sin∠ABP=$\frac{h}{PB}$=$\frac{\frac{\sqrt{2}}{2}}{\sqrt{5}}$=$\frac{\sqrt{10}}{10}$.
点评 本题考查了二次函数图象的几何变换,待定系数法求二次函数解析式,要求熟练掌握平移的规律:左加右减,上加下减.并用规律求函数解析式.会利用方程求抛物线与坐标轴的交点.

| A. | a2+a2=a4 | B. | (2a2)3=6a6 | C. | a8÷a2=a4 | D. | a3•a4=a7 |
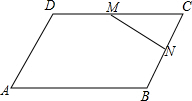 如图,在平行四边形ABCD中,点M是边CD中点,点N是边BC上的点,且$\frac{CN}{BN}$=$\frac{1}{2}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{MN}$可用$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$.
如图,在平行四边形ABCD中,点M是边CD中点,点N是边BC上的点,且$\frac{CN}{BN}$=$\frac{1}{2}$.设$\overrightarrow{AB}$=$\overrightarrow{a}$,$\overrightarrow{BC}$=$\overrightarrow{b}$,那么$\overrightarrow{MN}$可用$\overrightarrow{a}$、$\overrightarrow{b}$表示为$\frac{1}{2}$$\overrightarrow{a}$-$\frac{1}{3}$$\overrightarrow{b}$. 如图,在△ABC中,三条高AD,BE,CF相交于一点O,求∠1+∠2+∠3的度数.
如图,在△ABC中,三条高AD,BE,CF相交于一点O,求∠1+∠2+∠3的度数.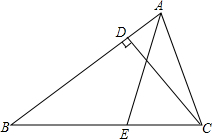 如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数.
如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数.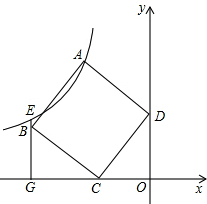 如图,正方形ABCD中,C(-3,0),D(0,4).过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.
如图,正方形ABCD中,C(-3,0),D(0,4).过B点作x轴的垂线交过A点的反比例函数图象于E点,交x轴于G点.