题目内容
20．
如图，已知△ABC≌△ADE，且∠CAD=10°，∠B=∠D=25°，∠EAB=125°，求∠DFB和∠DGB的度数．
分析 根据全等得出∠EAD=∠CAB，求出∠CAB=∠EAD=57.5°，根据三角形外角性质得出∠DFB=∠B+∠DAB，代入求出∠DFB，再根据三角形的外角性质得出∠DGF=∠DFB-∠D，代入求出即可．
解答 解：∵△ABC≌△ADE，
∴∠EAD=∠CAB，
∵∠CAD=10°，∠EAB=125°，
∴∠CAB=∠EAD=$\frac{1}{2}$（125°-10°）=57.5°，
∵∠B=25°，
∴∠DFB=∠B+∠DAB=25°+57.5°+10°=92.5°，
∵∠D=25°，
∴∠DGF=∠DFB-∠D=92.5°-25°=67.5°．
点评 本题考查了全等三角形的性质，三角形的外角性质的应用，解此题的关键是求出∠EAD=∠CAB，∠DFB=∠B+∠CAB，∠DGF=∠DFB-∠D，注意：全等三角形的对应角相等，三角形的一个外角等于和它不相邻的两个内角的和，难度适中．
练习册系列答案
暑假作业海燕出版社系列答案
相关题目
10．在△ABC中，∠C=90°，∠B=50°，AB=10，则BC的长为（ ）
| A． | 10tan50° | B． | 10sin40° | C． | 10sin50° | D． | $\frac{10}{cos50°}$ |
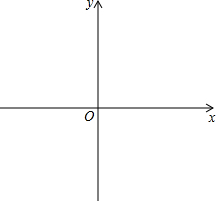已知：在直角坐标系中，直线y=x+1与x轴交于点A，与y轴交于点B，抛物线y=$\frac{1}{2}$（x-m）2+n的顶点D在直线AB上，与y轴的交点为C
如图，在正方形ABCD中，AB=a，M为AB的中点，ED=3AE．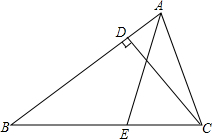
如图所示，AE为△ABC的角平分线，CD为△ABC的高，若∠B=30°，∠ACB为75°，求∠AFC的度数．
如图，直线AB∥CD，直线l分别交AB、CD于点E、F，EM平分∠BEF，∠EFD=50°，∠MEN=90°，求∠NEF的度数．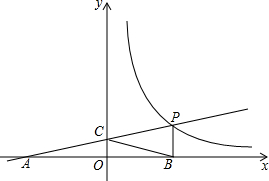
如图，点P为直线y=kx+b与双曲线y=$\frac{m}{x}$（x＞0）的交点，过点P作PB⊥x轴于点B，PB=2，直线y=kx+b与x轴交于点A（-4，0），与y轴交于点C，且AC=BC．