题目内容
15.(1)计算:cos245°+tan30°•sin60°(2)计算:($\sqrt{3}$-1)0-$\frac{\sqrt{12}cos30°}{tan45°}$+($\frac{1}{3}$)-2.
分析 (1)根据特殊角的三角函数值得到原式=($\frac{\sqrt{2}}{2}$)2+$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$,然后进行二次根式的乘法运算后合并即可;
(2)根据零指数幂、负整数指数幂和特殊角的三角函数值得到原式=1-$\frac{2\sqrt{3}•\frac{\sqrt{3}}{2}}{1}$+9,然后进行二次根式的乘法运算后合并即可.
解答 解:(1)原式=($\frac{\sqrt{2}}{2}$)2+$\frac{\sqrt{3}}{3}$×$\frac{\sqrt{3}}{2}$
=$\frac{1}{2}$+$\frac{1}{2}$
=1;
(2)原式=1-$\frac{2\sqrt{3}•\frac{\sqrt{3}}{2}}{1}$+9
=1-3+9
=7.
点评 本题考查了二次根式的计算:先把各二次根式化为最简二次根式,再进行二次根式的乘除运算,然后合并同类二次根式.也考查了零指数幂、负整数指数幂和特殊角的三角函数值.

练习册系列答案
 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案
相关题目
10.在△ABC中,∠C=90°,∠B=50°,AB=10,则BC的长为( )
| A. | 10tan50° | B. | 10sin40° | C. | 10sin50° | D. | $\frac{10}{cos50°}$ |
20.下列计算正确的是( )
| A. | a2+a2=a4 | B. | (2a2)3=6a6 | C. | a8÷a2=a4 | D. | a3•a4=a7 |
7.某校数学兴趣小组同学的年龄情况如表:
则这个小组同学的平均年龄为14岁.
| 年龄(岁) | 12 | 13 | 14 | 15 |
| 人数 | 1 | 3 | 3 | 5 |
4.已知a,b,c分别是△ABC的三边长,且满足2a4+2b4+c4=2a2c2+2b2c2,则△ABC是( )
| A. | 等腰三角形 | B. | 等腰直角三角形 | ||
| C. | 直角三角形 | D. | 等腰三角形或直角三角形 |
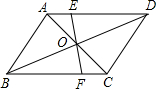 如图,?ABCD的对角线AC,BD相交于点O,过点O的直线分别与AD,BC相交于点E,F,写出图中关于点O成中心对称的三角形,四边形.
如图,?ABCD的对角线AC,BD相交于点O,过点O的直线分别与AD,BC相交于点E,F,写出图中关于点O成中心对称的三角形,四边形.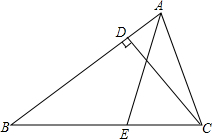 如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数.
如图所示,AE为△ABC的角平分线,CD为△ABC的高,若∠B=30°,∠ACB为75°,求∠AFC的度数.