题目内容
2. P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
分析 由△ABP绕B顺时针旋转90°得到△CBE,根据旋转的性质得到∠PBE=90°,BP=BE=a,即△BPE为等腰直角三角形,利用勾股定理得到PE2的值,即为以PE为边长的正方形的面积.
解答 解:∵△ABP绕B顺时针旋转90°得到△CBE,
∴∠PBE=90°,BP=BE=a,
即△BPE为等腰直角三角形,
∴PE2=BP2+BE2=a2+a2=2a2,
∴以PE为边长的正方形的面积=PE2=2a2.
点评 本题考查了旋转的性质,旋转前后的两个图形全等,对应点与旋转中心的连线段的夹角等于旋转角,对应点到旋转中心的距离相等.同时考查了正方形的性质和等腰直角三角形的性质.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
10.小明和小凡是同班同学,被分到了同一个学习小组.在一次数学活动课上,他们各自用一张面积为100cm2的正方形纸片制作了一副七巧板,并合作完成了如图所示的作品.请计算图中打圈部分的面积是( )
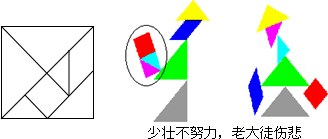

| A. | 12.5cm2 | B. | 25cm2 | C. | 37.5cm2 | D. | 50cm2 |
12.计算249×(-2)50所得的结果是( )
| A. | -2 | B. | 2 | C. | -299 | D. | 299 |
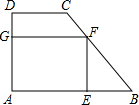 如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.
如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.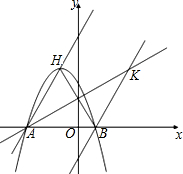 已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$对称.
已知,如图,二次函数y=ax2+2ax-3a(a≠0)图象的顶点为H,与x轴交于A、B两点(B在A点右侧),点H、B关于直线l:y=$\frac{\sqrt{3}}{3}$x+$\sqrt{3}$对称.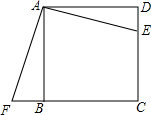 如图,E是边长为1的正方形ABCD中CD边上一点,CD=$\sqrt{3}$DE,△ABF是由△ADE顺时针旋转而成的图形
如图,E是边长为1的正方形ABCD中CD边上一点,CD=$\sqrt{3}$DE,△ABF是由△ADE顺时针旋转而成的图形 如图,正方形OPMN和正方形ABCD全等,AC与BD交于点O,正方形0PNM绕点O旋转,0M交AB于点E,OP交BC于F,如果正方形的边长为3,在上述旋转过程中,OE与0F有怎样的数量关系?四边形OEBF的面积有何变化?请证明你的发现.
如图,正方形OPMN和正方形ABCD全等,AC与BD交于点O,正方形0PNM绕点O旋转,0M交AB于点E,OP交BC于F,如果正方形的边长为3,在上述旋转过程中,OE与0F有怎样的数量关系?四边形OEBF的面积有何变化?请证明你的发现.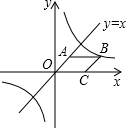 如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是$\sqrt{2}$.若反比例函数y=$\frac{k}{x}$的图象经过点B,则此反比例函数表达式中的k为$\sqrt{2}$+1.
如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是$\sqrt{2}$.若反比例函数y=$\frac{k}{x}$的图象经过点B,则此反比例函数表达式中的k为$\sqrt{2}$+1.