题目内容
13.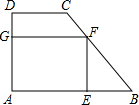 如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.
如图,在梯形ABCD中,AB∥CD,∠A=90°,AB=7,CD=4,AD=2,在梯形中作一个矩形AEFG,使E在AB上,F在BC上,G在AD上.(1)设EF=x,求△BEF的面积S;
(2)写出(1)中x的取值范围.
分析 (1)如图,过点C作CM⊥AB于M,得到四边形AMCD是矩形,求得CM=AD=2,得到BM=AB-AM=-4=3,通过△BEF∽△BMC,根据相似三角形的性质得到$\frac{BE}{EF}=\frac{BM}{CM}$=$\frac{3}{2}$,求得BE=$\frac{3}{2}$x,根据三角形的面积公式即可得到结论;
(2)由于AD=2,EF<AD,于是得到x的取值范围是:0<x<2.
解答  解:(1)如图,过点C作CM⊥AB于M,
解:(1)如图,过点C作CM⊥AB于M,
∵AB∥DC,∠A=90°,
∴四边形AMCD是矩形,
∴CM=AD=2,
∴AM=DC=4,
∴BM=AB-AM=-4=3,
∵EF∥CM,
∴△BEF∽△BMC,
∴$\frac{BE}{EF}=\frac{BM}{CM}$=$\frac{3}{2}$,
∴BE=$\frac{3}{2}$x,
∴△BEF的面积S=$\frac{1}{2}$BE•EF=$\frac{1}{2}•$$\frac{3}{2}$x•x=$\frac{3}{4}$x2;
(2)∵AD=2,EF<AD,
∴x的取值范围是:0<x<2.
点评 本题考查了相似三角形的判定和性质,矩形的性质,三角形面积的求法,正确的作出辅助线构造相似三角形是解题的关键.

练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案
相关题目
3.下列各式正确的是( )
| A. | -27>-17 | B. | -5-4=-1 | C. | -|-2-1|=-3 | D. | (-25)÷(-5)×0=5 |
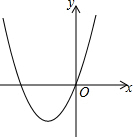 已知抛物线的顶点为(-2,-3),且经过原点,
已知抛物线的顶点为(-2,-3),且经过原点, 表示a-b+c,图形
表示a-b+c,图形 表示-x+y-z,则
表示-x+y-z,则 +
+ 的值为-3.
的值为-3.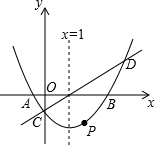 如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.
如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.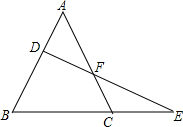 如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.
如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.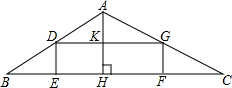 如图,矩形DEFG内接于△ABC,AH⊥BC,DG与AH相交于点K,BC=48,高AH=16.
如图,矩形DEFG内接于△ABC,AH⊥BC,DG与AH相交于点K,BC=48,高AH=16. P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.