题目内容
15.(1)平面直角坐标系中,若以动点P(x,y)到点F(0,1)的距离与点P到直线y=-1的距离相等,满足要求的动点P在某一条抛物线上,则此抛物线的解析式为y=$\frac{{x}^{2}}{4}$.(2)已知该平面内还有一定点A(-1,2),连接PF、PA、FA,当△PAF的周长最小时,点P的坐标为(-1,$\frac{1}{4}$).
分析 (1)根据勾股定理求出P到F的距离,再根据P到F的距离为y+1,列出方程,得到抛物线的解析式;
(2)△PAF的周长=PF+AF+PA,由于AF为定值,所以当PF+PA最小时,△PAF的周长最小,由PE=PF,所以当PA、PE在同一直线上,可求出P的坐标.
解答 解:(1)设P(x,y),则
PF=$\sqrt{{x}^{2}+(y-1)^{2}}$,
∵P到F的距离为y+1,
∴y+1=$\sqrt{{x}^{2}+(y-1)^{2}}$,
∴y=$\frac{{x}^{2}}{4}$;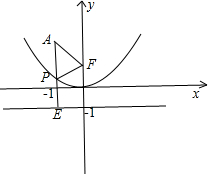
(2)∵△PAF的周长=PF+AF+PA,AF为定值,
∴当PF+PA最小时,△PAF的周长最小,
∵PE=PF,
∴PF+PA=PE+PA最小,
当PA、PE在同一直线上,AE⊥x轴,
∵点A(-1,2),
∴P的横坐标为-1,
y=$\frac{(-1)^{2}}{4}$=$\frac{1}{4}$,
∴P(-1,$\frac{1}{4}$).
故答案为:(1)y=$\frac{{x}^{2}}{4}$,(2)(-1,$\frac{1}{4}$).
点评 本题主要考查了坐标与图形的性质以及最短路径问题,数形结合,正确理解题意是解决问题的关键.

练习册系列答案
相关题目
5.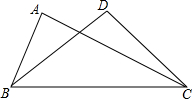 如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )
如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )
 如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )
如图,在△ABC和△DCB中,AB=DC,下列四个条件:①AC=DB;②∠A=∠B; ③∠ABC=∠DCB;④∠ACB=∠DBC中,添加其中的一个条件不能使△ABC≌△DCB的有( )| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
3.下列去括号中正确的是( )
| A. | x-(2x+y-1)=x-2x+y-1 | B. | 3x2-3(x+6)=3x2-3x-6 | ||
| C. | 5a2+(-3a-b)-(2c-d)=5a2-3a-b-2c+d | D. | x-[y-(x+1)]=x-y-z-1 |
20.下列各组数的比较大小中,不正确的是( )
| A. | -$\frac{6}{5}>-(-\frac{3}{5})$ | B. | -(+3)<-(-4) | C. | 0>-|-3| | D. | +(-2)<-(-1) |
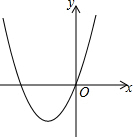 已知抛物线的顶点为(-2,-3),且经过原点,
已知抛物线的顶点为(-2,-3),且经过原点, 表示a-b+c,图形
表示a-b+c,图形 表示-x+y-z,则
表示-x+y-z,则 +
+ 的值为-3.
的值为-3.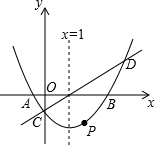 如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.
如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点. P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.