题目内容
11.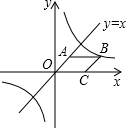 如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是$\sqrt{2}$.若反比例函数y=$\frac{k}{x}$的图象经过点B,则此反比例函数表达式中的k为$\sqrt{2}$+1.
如图所示,已知菱形OABC,点C在x轴上,直线y=x经过点A,菱形OABC的面积是$\sqrt{2}$.若反比例函数y=$\frac{k}{x}$的图象经过点B,则此反比例函数表达式中的k为$\sqrt{2}$+1.
分析 作AH⊥x轴于H,如图,利用一次函数图象上点的坐标特征,设A(t,t),利用菱形面积公式得到OC=$\frac{\sqrt{2}}{t}$,则可表示出B(t+$\frac{\sqrt{2}}{t}$,t),然后利用反比例函数函数图象上点的坐标特征可计算出k的值.
解答 解:作AH⊥x轴于H,如图,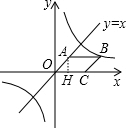
设A(t,t),
∵菱形OABC的面积是$\sqrt{2}$,
∴t•OC=$\sqrt{2}$,
∴OC=$\frac{\sqrt{2}}{t}$,
∵四边形OABC为菱形,
∴AB=$\frac{\sqrt{2}}{t}$,AB∥x轴,
∴B(t+$\frac{\sqrt{2}}{t}$,t),
而B(t+$\frac{\sqrt{2}}{t}$,t)在反比例函数函数y=$\frac{k}{x}$的图象上,
∴k=(t+$\frac{\sqrt{2}}{t}$)•t=$\sqrt{2}$+1.
故答案为$\sqrt{2}$+1.
点评 本题考查了反比例函数的比例系数k的几何意义:在反比例函数y=kx图象中任取一点,过这一个点向x轴和y轴分别作垂线,与坐标轴围成的矩形的面积是定值|k|.也考查了菱形的性质.

练习册系列答案
 同步轻松练习系列答案
同步轻松练习系列答案 课课通课程标准思维方法与能力训练系列答案
课课通课程标准思维方法与能力训练系列答案
相关题目
19.下列图案中不能由一个图形通过旋转而构成的有( )
| A. |  | B. |  | C. |  | D. |  |
16.用配方法解方程x2-4x+2=0,下列配方正确的是( )
| A. | (x-4)2=14 | B. | (x+4)2=14 | C. | (x+2)2=2 | D. | (x-2)2=2 |
3.下列各式正确的是( )
| A. | -27>-17 | B. | -5-4=-1 | C. | -|-2-1|=-3 | D. | (-25)÷(-5)×0=5 |
1.下列方程是一元二次方程的是( )
| A. | x2-2=0 | B. | 2x3+3=5 | C. | $3x+\frac{1}{x}=4$ | D. | x+2y=4 |
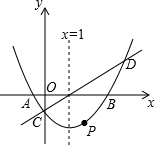 如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点.
如图,在直角坐标系中,抛物线y=$\frac{1}{3}$x2-mx+n与x轴交于A,B两点,与y轴交于点C,且对称轴是直线x=1.直线y=x-1与抛物线y=$\frac{1}{3}$x2-mx+n相交于C,D两点.点P是抛物线上的动点. P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.