题目内容
7.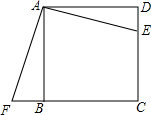 如图,E是边长为1的正方形ABCD中CD边上一点,CD=$\sqrt{3}$DE,△ABF是由△ADE顺时针旋转而成的图形
如图,E是边长为1的正方形ABCD中CD边上一点,CD=$\sqrt{3}$DE,△ABF是由△ADE顺时针旋转而成的图形(1)∠FAB的度数是多少?
(2)连接EF,△AEF的面积是多少?
(3)若把△ADE逆时针同样的度数而成△AD′E′,AE的中点M,M′是M的对应点,求MM′的长.
分析 (1)由四边形ABCD为正方形,得到AD=AB,∠DAB=90°,又△ADE绕点A顺时针旋转后与△ABF重合,则∠DAE等于∠BAF,根据CD=$\sqrt{3}$DE,可得tan∠DAE=$\frac{DE}{AD}$,即可得到∠FAB的角度.
(2)证得△AEF是等腰直角三角形,根据勾股定理求得AE2=$\frac{4}{3}$,然后根据三角形的面积公式即可求得;
(3)证得△AEE′是等腰直角三角形,根据勾股定理求得EE′的长,然后根据中位线定理即可求得.
解答 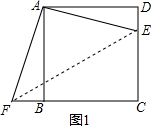 解:(1)如图1,∵四边形ABCD为正方形,
解:(1)如图1,∵四边形ABCD为正方形,
∴AD=AB,∠DAB=90°,
又∵△ADE绕点A顺时针旋转后与△ABF重合,
∴∠DAB=∠EAF=90°,
∵CD=$\sqrt{3}$DE,
∴tan∠DAE=$\frac{DE}{AD}$=$\frac{1}{\sqrt{3}}$=$\frac{\sqrt{3}}{3}$,
∴∠DAE=30°,
∴∠FAB=30°.
(2)如图1,连接EF,
∵∠DAE=∠FAB=30°,
∴∠FAE=90°,
∵AF=AE,
∴△AEF是等腰直角三角形,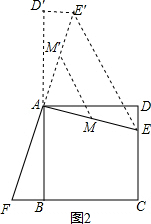
∵AD=1,AD=CD=$\sqrt{3}$DE,
∴DE=$\frac{\sqrt{3}}{3}$,
∴AE2=AD2+DE2=12+($\frac{\sqrt{3}}{3}$)2=$\frac{4}{3}$,
∵S△AEF=$\frac{1}{2}$AE•AF=$\frac{1}{2}$AE2,
∴S△AEF=$\frac{2}{3}$;
(3)同理△AEE′是等腰直角三角形,
如图2,∴EE′2=2AE2=$\frac{8}{3}$,
∴EE′=$\frac{2\sqrt{6}}{3}$,
∵MM′是△AEE′的中位线,
∴MM′=$\frac{1}{2}$EE′=$\frac{\sqrt{6}}{3}$.
点评 本题考查了旋转的性质,正方形的性质,等腰直角三角形的判定,勾股定理的应用以及三角函数,熟练掌握旋转的性质是解题的关键.

| A. | -$\frac{6}{5}>-(-\frac{3}{5})$ | B. | -(+3)<-(-4) | C. | 0>-|-3| | D. | +(-2)<-(-1) |
| A. |  | B. |  | C. |  | D. |  |
| A. | (x-4)2=14 | B. | (x+4)2=14 | C. | (x+2)2=2 | D. | (x-2)2=2 |
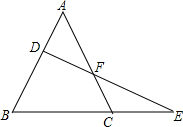 如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.
如图,△ABC中,直线DE交AB于D,交AC于F,交BC的延长线于E,求证:$\frac{AD}{DB}$•$\frac{BE}{EC}$•$\frac{CF}{FA}$=1.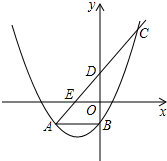 如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点,
如图,抛物线y=ax2+2ax+c与直线y=x+b交于A(-2,-1)、C(1,2)两点,与y轴交于B,D、E是直线y=x+b与坐标轴的交点, P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.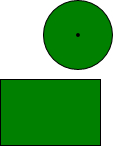 这是公园里两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分,如果你是设计师,你怎样设计这条小路?
这是公园里两块形状不同的草坪,现在要修一条笔直的小路同时穿过这两块草坪,而且同时把两块草坪分成面积相同的两部分,如果你是设计师,你怎样设计这条小路?