题目内容
14. 如图,正方形OPMN和正方形ABCD全等,AC与BD交于点O,正方形0PNM绕点O旋转,0M交AB于点E,OP交BC于F,如果正方形的边长为3,在上述旋转过程中,OE与0F有怎样的数量关系?四边形OEBF的面积有何变化?请证明你的发现.
如图,正方形OPMN和正方形ABCD全等,AC与BD交于点O,正方形0PNM绕点O旋转,0M交AB于点E,OP交BC于F,如果正方形的边长为3,在上述旋转过程中,OE与0F有怎样的数量关系?四边形OEBF的面积有何变化?请证明你的发现.
分析 根据正方形的性质,利用ASA即可证明△AOE≌△BOF,从而可知S四边形OEBF=S△AOB=$\frac{1}{4}$S正方形ABCD.可以得到在旋转的过程中四边形OEBF的面积不变化.
解答 OE=OF,四边形OEBF的面积不变.
证明:∵∠AOE+∠BOE=90°,∠MOP=90°,
∴∠BOF=∠AOE,
在△OAE和△OBF中,
$\left\{\begin{array}{l}{∠OAE=∠OBF=45°}\\{OA=OB}\\{∠AOE=∠BOF}\end{array}\right.$,
∴△AOE≌△BOF,
∴S△AOE=S△BOF.OE=OF,
∴S△AOE+S△OBE=S△BOF+S△OBE,
即S△AOB=S四边形OEBF,
∵S△AOB=$\frac{1}{2}$OA•OB=$\frac{1}{2}$×$\frac{AB}{\sqrt{2}}$×$\frac{AB}{\sqrt{2}}$=$\frac{1}{4}$×32=$\frac{9}{4}$,
∴S四边形OEBF=$\frac{9}{4}$.
点评 本题考查了图形的旋转,求解时需抓住正方形的特征,找出△AOE与△BOF在旋转过程中的对称性,获得四边形OEBF的面积与正方形面积的关系,关键是将四边形OEBF的面积转化为△OAB的面积.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
19.下列图案中不能由一个图形通过旋转而构成的有( )
| A. |  | B. |  | C. |  | D. |  |
3.下列各式正确的是( )
| A. | -27>-17 | B. | -5-4=-1 | C. | -|-2-1|=-3 | D. | (-25)÷(-5)×0=5 |
 表示a-b+c,图形
表示a-b+c,图形 表示-x+y-z,则
表示-x+y-z,则 +
+ 的值为-3.
的值为-3.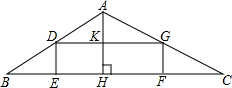 如图,矩形DEFG内接于△ABC,AH⊥BC,DG与AH相交于点K,BC=48,高AH=16.
如图,矩形DEFG内接于△ABC,AH⊥BC,DG与AH相交于点K,BC=48,高AH=16. P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.
P为正方形ABCD内一点,将△ABP绕B顺时针旋转90°到△CBE的位置,若BP=a.求:以PE为边长的正方形的面积.