题目内容
3.解方程:$\frac{5x-4}{2x-4}$+$\frac{1}{2}$=$\frac{2x+5}{3x-6}$.分析 分式方程去分母转化为整式方程,求出整式方程的解得到x的值,经检验即可得到分式方程的解.
解答 解:由原方程,得
3(5x+4)+3(x-2)=2(2x+5),
整理,得7x-2=0,
解得x=$\frac{2}{7}$,
经检验,x=$\frac{2}{7}$是原方程的解.
所以原方程的解是x=$\frac{2}{7}$.
点评 此题考查了解分式方程,解分式方程的基本思想是“转化思想”,把分式方程转化为整式方程求解.解分式方程一定注意要验根.

练习册系列答案
 中考解读考点精练系列答案
中考解读考点精练系列答案
相关题目
12. 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
 如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )
如图,在菱形ABCD中,AB=5,∠B:∠BCD=1:2,则对角线AC等于( )| A. | 5 | B. | 10 | C. | 15 | D. | 20 |
13.已知直角三角形的两条直角边的边长为3和4,则它的斜边长C是( )
| A. | 5 | B. | $\sqrt{7}$ | C. | 5或$\sqrt{7}$ | D. | 1<C<7 |
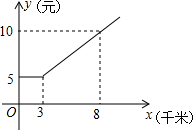 某歌唱大赛已经拉开序幕,欢欢准备乘坐出租车去比赛现场观看比赛,如图是乘坐出租车费用y(元)与路程x(千米)之间的函数图象.
某歌唱大赛已经拉开序幕,欢欢准备乘坐出租车去比赛现场观看比赛,如图是乘坐出租车费用y(元)与路程x(千米)之间的函数图象.