题目内容
16.阅读下面材料:在数学课上,老师请同学思考如下问题:

小轩的主要作法如下:

老师说:“小轩的作法正确.”
请回答:⊙P与BC相切的依据是角平分线上的点到角两边距离相等,若圆心到直线的距离等于半径,则这条直线为圆的切线.
分析 作PD⊥BC,根据角平分线上的点到角两边的距离相等,易得PD=PA,根据切线的判定定理可证得BC是⊙P的切线.
解答  证明:作PD⊥BC,
证明:作PD⊥BC,
∵BF平分∠ABC,∠A=90°
∴PA=PD,
∴PD是⊙P的半径,
∴D在⊙P上,
∴BC是⊙P的切线.
故答案为:角平分线上的点到角两边距离相等,若圆心到直线的距离等于半径,则这条直线为圆的切线.
点评 本题考查了作图-复杂作图:复杂作图是在五种基本作图的基础上进行作图,一般是结合了几何图形的性质和基本作图方法.解决此类题目的关键是熟悉基本几何图形的性质,结合几何图形的基本性质把复杂作图拆解成基本作图,逐步操作.也考查了切线的判定.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
7.将分式方程$\frac{2}{x-2}=\frac{1}{x}$去分母后得到正确的整式方程是( )
| A. | x-2=x | B. | x2-2x=2x | C. | x-2=2x | D. | x=2x-4 |
 已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.
已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.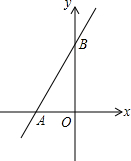 如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).
如图,平面直角坐标系中,点O为坐标原点,一次函数的图象过点(-1,4)与点(3,12).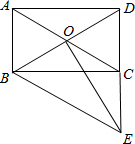 如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.
如图,矩形ABCD的对角线AC,BD相交于点O,过点B作AC的平行线交DC的延长线于点E.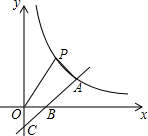 如图,一次函数y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,m),与x轴、y轴分别交于B、C两点,C点坐标为(0,-1).
如图,一次函数y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,m),与x轴、y轴分别交于B、C两点,C点坐标为(0,-1).