题目内容
1.已知?ABCD中,AB=4,∠ABC与∠DCB的角平分线交AD边于点E,F,且EF=3,则边AD的长为11或5.分析 由平行四边形的性质和角平分线的定义证出∠ABE=∠AEB,得出AE=AB=4,同理:DF=CD=4,再分两种情况计算即可.
解答 解:∵BE平分∠ABC,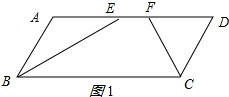
∴∠ABE=∠CBE,
∵四边形ABCD是平行四边形,
∴AD∥CB,CD=AB=4,
∴∠AEB=∠CBE
∴∠ABE=∠AEB,
∴AE=AB=4,
同理:DF=CD=4,
分两种情况: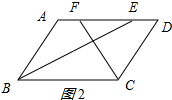
①如图1所示:∵EF=3,
∴AD=AE+EF+DF=4+3+4=11;
②如图2所示:∵EF=4,AE=DF=4,
∴AF=1,∴AD=AF+DF=1+4=5;
综上所述:AD的长为11或5;
故答案为:11或5.
点评 此题主要考查了角平分线的定义、平行四边形的性质、平行线的性质、等腰三角形的判定等知识;熟练掌握平行四边形的性质,证明三角形是等腰三角形是解决问题的关键.

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目


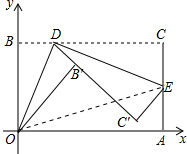 如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.
如图,将矩形纸片ABCD置于直角坐标系中,点A(4,0),点B(0,3),点D(异于点B、C)为边BC上动点,过点O、D折叠纸片,得点B′和折痕OD.过点D再次折叠纸片,使点C落在直线DB′上,得点C′和折痕DE,连接OE,设BD=t.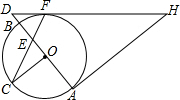 如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D.
如图,在⊙O中,AB为直径,OC⊥AB,弦CF与OB交于点E,过点F,A分别作⊙O的切线交于点H,且HF与AB的延长线交于点D. 如图,在Rt△ABC中,∠BAC=90°,AB=AC.
如图,在Rt△ABC中,∠BAC=90°,AB=AC.