题目内容
6.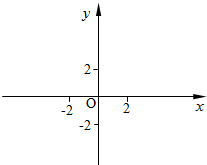 已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.
已知一条直线y=kx+b在y轴上的截距为2,它与x轴、y轴的交点分别为A、B,且△ABO的面积为4.(1)求点A的坐标;
(2)若k<0,在直角坐标平面内有一点D,使四边形ABOD是一个梯形,且AD∥BO,其面积又等于20(平方单位),试求点D的坐标.
分析 (1)根据题意得出点B的坐标,利用三角形的面积得出点A的坐标即可;
(2)根据梯形的面积解答即可.
解答 (1)解:设点A的坐标为(x,0)
由题意,得:b=2,点B的坐标为(0,2),
所以${S_{△ABO}}=\frac{1}{2}×OA×OB=\frac{1}{2}×|x|×2=4$,
解得:x=±4
所以点A的坐标为(4,0)或(-4,0);
(2)解:因为k<0
所以点 A的坐标为(4,0),OA=4,
∵AD∥OB,OB⊥OA
∴${S_{梯形ABOD}}=\frac{1}{2}×(OB+AD)×OA=\frac{1}{2}(2+AD)×4=20$,
∴AD=8,
根据题意可知:点D在第四象限
∴点D的坐标为(4,-8).
点评 此题考查了梯形的问题,关键是根据一次函数图象上点的坐标特征解答.

练习册系列答案
相关题目
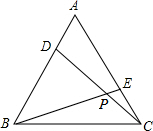 如图,D、E分别是等边三角形ABC的两边AB、AC上的点,且AD=CE,BE,DC相交于点P,则∠BPD的度数为60°.
如图,D、E分别是等边三角形ABC的两边AB、AC上的点,且AD=CE,BE,DC相交于点P,则∠BPD的度数为60°.