题目内容
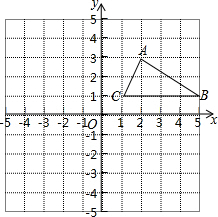 如图在12×12的正方形网格中建立坐标系,△ABC顶点都在边长为1的小正方形的格点上.
如图在12×12的正方形网格中建立坐标系,△ABC顶点都在边长为1的小正方形的格点上.(1)点A坐标是
(2)画出△ABC关于y轴对称的△A1B1C1.
(3)在x轴正半轴上找一点D,使得以D、B、C为顶点的三角形是等腰三角形,请直接写出符合条件的点D坐标.
考点:作图-轴对称变换,等腰三角形的判定
专题:作图题
分析:(1)根据平面直角坐标系写出即可;
(2)根据网格结构找出点A1、B1、C1的位置,然后顺次连接即可;
(3)分BC是底边和腰长两种情况讨论求解.
(2)根据网格结构找出点A1、B1、C1的位置,然后顺次连接即可;
(3)分BC是底边和腰长两种情况讨论求解.
解答:解:(1)A(2,3);
故答案为:(2,3);
(2)△A1B1C1如图所示;

(3)BC是底边时,D(3,0),
BC是腰长时,由勾股定理得,
=
,
D(5-
,0)或D(1+
,0),
综上所述,点D的坐标为(3,0)或(5-
,0)或D(1+
,0).
故答案为:(2,3);
(2)△A1B1C1如图所示;

(3)BC是底边时,D(3,0),
BC是腰长时,由勾股定理得,
| 42-12 |
| 15 |
D(5-
| 15 |
| 15 |
综上所述,点D的坐标为(3,0)或(5-
| 15 |
| 15 |
点评:本题考查了利用轴对称变换作图,等腰三角形的性质,熟练掌握网格结构准确找出对应点的位置是解题的关键,难点在于(3)分情况讨论.

练习册系列答案
相关题目
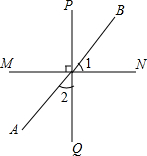 如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )
如图,直线PQ⊥MN,垂足为O,AB是过点O的直线,∠1=50°,则∠2的度数为( )| A、50° | B、40° |
| C、60° | D、70° |
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )| A、15° | B、25° |
| C、10° | D、20° |
 如图,∠AOB=68°,OC平分∠AOB,则∠BOC的度数为
如图,∠AOB=68°,OC平分∠AOB,则∠BOC的度数为 如图,⊙O是△ABC的外接圆,∠A=40°,则∠OCB等于
如图,⊙O是△ABC的外接圆,∠A=40°,则∠OCB等于 如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求:
如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求: 某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为s1(米),s2(米),则s1,s2与t的函数关系如图,试根据图象解决下列问题:
某学校开展“青少年科技创新比赛”活动,“喜洋洋”代表队设计了一个遥控车沿直线轨道AC做匀速直线运动的模型.甲、乙两车同时分别从A,B出发,沿轨道到达C处,在AC上,甲的速度是乙的速度的1.5倍,设t(分)后甲、乙两遥控车与B处的距离分别为s1(米),s2(米),则s1,s2与t的函数关系如图,试根据图象解决下列问题: 如图,在△ABC中,AB=AC,BD=CD,求证:△ABD≌△ACD.
如图,在△ABC中,AB=AC,BD=CD,求证:△ABD≌△ACD.