题目内容
 如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )
如图,将Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,若∠B=60°,则∠1的度数是( )| A、15° | B、25° |
| C、10° | D、20° |
考点:旋转的性质
专题:计算题
分析:先利用互余计算出∠BAC=90°-∠B=30°,再根据旋转的性质得∠ACA′=90°,CA=CA′,∠CA′B′=∠CAB=30°,则可判断△ACA′为等腰直角三角形,则∠CA′A=45°,然后利用∠1=∠CA′A-∠CA′B′进行计算即可.
解答:解:∵∠ACB=90°,∠B=60°,
∴∠BAC=90°-∠B=30°,
∵Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,
∴∠ACA′=90°,CA=CA′,∠CA′B′=∠CAB=30°,
∴△ACA′为等腰直角三角形,
∴∠CA′A=45°,
∴∠1=∠CA′A-∠CA′B′=45°-30°=15°.
故选A.
∴∠BAC=90°-∠B=30°,
∵Rt△ABC绕直角顶点C顺时针旋转90°,得到△A′B′C,
∴∠ACA′=90°,CA=CA′,∠CA′B′=∠CAB=30°,
∴△ACA′为等腰直角三角形,
∴∠CA′A=45°,
∴∠1=∠CA′A-∠CA′B′=45°-30°=15°.
故选A.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了等腰直角三角形的判定与性质.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
如图,在下列四个几何体中,它的三视图(主视图、左视图、俯视图)完全相同的是 ( )


| A、①② | B、②③ | C、①④ | D、②④ |
 如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.
如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.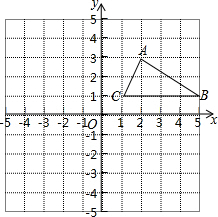 如图在12×12的正方形网格中建立坐标系,△ABC顶点都在边长为1的小正方形的格点上.
如图在12×12的正方形网格中建立坐标系,△ABC顶点都在边长为1的小正方形的格点上.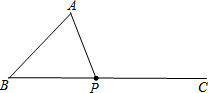 如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP=
如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP= 如图,在平面直角坐标系中,O是坐标原点,抛物线y=ax2+bx与x轴正半轴交于点A,对称轴DE交x轴于点E.点B在第二象限,过点B作BC⊥x轴于点C,连结AB,且AB=10,AC=8.将点B向右平移5个单位后,恰好与抛物线的顶点D重合.
如图,在平面直角坐标系中,O是坐标原点,抛物线y=ax2+bx与x轴正半轴交于点A,对称轴DE交x轴于点E.点B在第二象限,过点B作BC⊥x轴于点C,连结AB,且AB=10,AC=8.将点B向右平移5个单位后,恰好与抛物线的顶点D重合.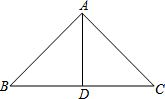 下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数.”
下面是小明同学在学了等腰三角形后所做的一道题,题目是这样的:“已知△ABC是等腰三角形,BC边上的高恰好等于BC边长的一半,求∠BAC的度数.”