题目内容
 如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求:
如图,△ABC中,∠ACB=90°,CD是高,AC=8,CB=6,AB=10,求:(1)三角形面积S△ABC;
(2)CD的长.
考点:三角形的面积
专题:
分析:(1)根据三角形的面积公式即可求得三角形面积S△ABC;
(2)根据三角形的面积S═
AB•CD,就可求得.
(2)根据三角形的面积S═
| 1 |
| 2 |
解答:解:(1)∵∠ACB=90°,AC=8,CB=6,
∴S△ABC=
CB•AC=
×6×8=24;
(2)∵△ABC中,∠ACB=90°,CD是高,
∴S△ABC=
AB•CD,
∴CD=
=
=
.
∴S△ABC=
| 1 |
| 2 |
| 1 |
| 2 |
(2)∵△ABC中,∠ACB=90°,CD是高,
∴S△ABC=
| 1 |
| 2 |
∴CD=
| 2S△ABC |
| AB |
| 2×24 |
| 10 |
| 24 |
| 5 |
点评:本题考查了直角三角形面积的不同表示方法,求解斜边上的高是解直角三角形的重要题型之一,也是中考的热点.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
下列方程是一元一次方程的是( )
| A、x+y=4 | ||
| B、3y=1 | ||
| C、x2-x-1=0 | ||
D、x+
|
下列比较大小:①
>
;②
>
;③
+1<5;④
<
.其中正确的是( )
| ||
| 2 |
| 2 |
1-
| ||
| 2 |
| 7 |
| 100 |
| 7 |
| ||
| 2 |
| 2 |
| A、①③ | B、③④ | C、①④ | D、②④ |
 如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.
如图,直线AB与CD相交于点O,射线OF,OD分别是∠AOE,∠BOE的角平分线.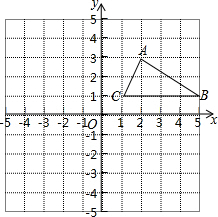 如图在12×12的正方形网格中建立坐标系,△ABC顶点都在边长为1的小正方形的格点上.
如图在12×12的正方形网格中建立坐标系,△ABC顶点都在边长为1的小正方形的格点上. 如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP=
如图,已知∠B=45°,AB=4cm,点P为∠ABC的边BC上一动点,则当BP= 如图,在平面直角坐标系中,O是坐标原点,抛物线y=ax2+bx与x轴正半轴交于点A,对称轴DE交x轴于点E.点B在第二象限,过点B作BC⊥x轴于点C,连结AB,且AB=10,AC=8.将点B向右平移5个单位后,恰好与抛物线的顶点D重合.
如图,在平面直角坐标系中,O是坐标原点,抛物线y=ax2+bx与x轴正半轴交于点A,对称轴DE交x轴于点E.点B在第二象限,过点B作BC⊥x轴于点C,连结AB,且AB=10,AC=8.将点B向右平移5个单位后,恰好与抛物线的顶点D重合. 将如图所示的“大箭头”按肩头所指的方向平移3厘米,请你作出平移后的图形.
将如图所示的“大箭头”按肩头所指的方向平移3厘米,请你作出平移后的图形. 如图,在△ABC中,AB=AC,∠A=120°,BC=8cm,AB的垂直平分线交BC于点M,交AB于点D,AC的垂直平分线交BC于点N,交AC于点E,求MN的长.
如图,在△ABC中,AB=AC,∠A=120°,BC=8cm,AB的垂直平分线交BC于点M,交AB于点D,AC的垂直平分线交BC于点N,交AC于点E,求MN的长.