题目内容
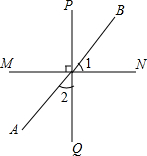如图，直线PQ⊥MN，垂足为O，AB是过点O的直线，∠1=50°，则∠2的度数为（ ）| A、50° | B、40° |
| C、60° | D、70° |
考点：垂线,对顶角、邻补角
专题：
分析：根据垂线的性质，可得∠PON的度数，根据角的和差，可得∠POB的度数，根据对顶角的性质，可得答案．
解答：解：由直线PQ⊥MN，垂足为O，得
∠PON=90°．
由角的和差，得∠POB=∠PON-∠1=90°-50°=40°，
由对顶角相等，得∠2=∠1=40°，
故选：B．
∠PON=90°．
由角的和差，得∠POB=∠PON-∠1=90°-50°=40°，
由对顶角相等，得∠2=∠1=40°，
故选：B．
点评：本题考查了垂线，利用了垂线的定义，角的和差，对顶角相等．
练习册系列答案
相关题目
关于x的一元二次方程2（x+4）2=a有两个相等的实数根，则a的取值范围是（ ）
| A、a≤0 | B、a≥0 |
| C、a＞0 | D、a=0 |
如图，直线AB与CD相交于点O，射线OF，OD分别是∠AOE，∠BOE的角平分线．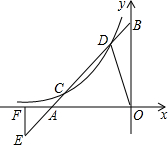
已知直线y=x+3与x轴、y轴分别交于A，B点，与y=
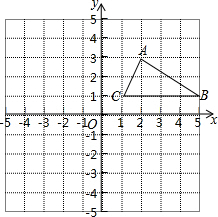如图在12×12的正方形网格中建立坐标系，△ABC顶点都在边长为1的小正方形的格点上．下列比较大小：①
＞
；②
＞
；③
+1＜5；④
＜
．其中正确的是（ ）
| ||
| 2 |
| 2 |
1-
| ||
| 2 |
| 7 |
| 100 |
| 7 |
| ||
| 2 |
| 2 |
| A、①③ | B、③④ | C、①④ | D、②④ |