题目内容
14. 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作AF∥BC,交CE的延长线于点F,且AF=BD,当AB与AC满足什么条件时,四边形AFBD是矩形?
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作AF∥BC,交CE的延长线于点F,且AF=BD,当AB与AC满足什么条件时,四边形AFBD是矩形?
分析 由AAS证明证明△AEF≌△DEC,得出AF=CD,证明四边形AFBD是平行四边形,再根据等腰三角形三线合一证明∠ADB=90°,进而根据有一个角是直角的平行四边形是矩形得证.
解答 解:AB=AC,理由如下:
∵AF∥BC,
∴∠AFE=∠DCE,
∵E为AD的中点,
∴EA=ED,
在△AEF和△DEC中,$\left\{\begin{array}{l}{∠AFE=∠DCE}&{\;}\\{∠AEF=∠DEC}&{\;}\\{EA=ED}&{\;}\end{array}\right.$,
∴△AEF≌△DEC(ASA);
∴AF=CD,
∵AF=BD,AF∥BC,
∴四边形AFBD是平行四边形,BD=CD,
∵AB=AC,
∴AD⊥BD,
∴四边形AFBD是矩形.
点评 本题考查了矩形的判定,三角形全等的判定及性质,平行四边形的判定;能够了解矩形的判定定理是解答本题的关键,难度不大.

练习册系列答案
 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案
相关题目
4.立方根等于2的数是( )
| A. | 4 | B. | 8 | C. | ±8 | D. | $\root{3}{2}$ |
5.△ABC∽△DEF,且相似比为2:1,△ABC的面积为8,则△DEF的面积为( )
| A. | 2 | B. | 4 | C. | 8 | D. | 16 |
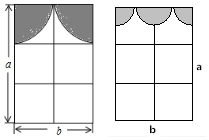 如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).
如图,小红和小兰房间窗户的装饰物分别由一些半圆和四分之一圆组成(半径分别相同).