题目内容
4.在正方形ABCD的平面内作等边三角形△ADE,则∠AEB的度数为75°.分析 根据正方形的性质求出∠BAD=90°,AB=AD,根据等边三角形性质求出∠EAD的度数和∠ABE=∠AEB,根据三角形的内角和定理求出即可.
解答 解:∵四边形ABCD是正方形,
∴∠BAD=90°,AB=AD,
∵△AED是等边三角形,
∴∠EAD=60°,AD=AE=AB,
∴∠BAE=90°-60°=30°,
∠ABE=∠AEB=$\frac{1}{2}$(180°-∠BAE)=75°.
故答案为:75°.
点评 本题考查了三角形的内角和定理、等腰三角形的性质,等边三角形的性质、正方形的性质的知识点的应用,关键是求出∠EAD的度数和证出∠ABE=∠AEB.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
19. 如图是一个正方体的表面展开图,这个正方体可能是( )
如图是一个正方体的表面展开图,这个正方体可能是( )
 如图是一个正方体的表面展开图,这个正方体可能是( )
如图是一个正方体的表面展开图,这个正方体可能是( )| A. |  | B. |  | C. |  | D. |  |
13.已知点A(3,-2)和点B关于y轴对称,则点B的坐标是( )
| A. | (3,2) | B. | (-3,-2) | C. | (-2,-3) | D. | (-3,2) |
 如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作AF∥BC,交CE的延长线于点F,且AF=BD,当AB与AC满足什么条件时,四边形AFBD是矩形?
如图,在△ABC中,D是BC边上的一点,E是AD的中点,过点A作AF∥BC,交CE的延长线于点F,且AF=BD,当AB与AC满足什么条件时,四边形AFBD是矩形? 已知:如图,QA切⊙O于点A,QB交⊙O于B和C两点,P是$\widehat{BC}$上任意一点,∠P=105°,∠AOC=64°,求∠Q的度数.
已知:如图,QA切⊙O于点A,QB交⊙O于B和C两点,P是$\widehat{BC}$上任意一点,∠P=105°,∠AOC=64°,求∠Q的度数. 如图,△ABC≌△DCB,点A、B的对应顶点分别为点D、C,如果AB=7cm,BC=12cm,AC=9cm,那BD的长是9cm.
如图,△ABC≌△DCB,点A、B的对应顶点分别为点D、C,如果AB=7cm,BC=12cm,AC=9cm,那BD的长是9cm.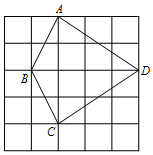 如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,求四边形ABCD的周长.(结果化为最简二次根式).
如图,5×5网格的每个小正方形的边长均为1,每个小正方形的顶点叫做格点,四边形ABCD的顶点A、B、C、D均在格点上,求四边形ABCD的周长.(结果化为最简二次根式).