题目内容
6.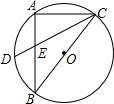 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )| A. | 7:2 | B. | 5:2 | C. | 4:1 | D. | 3:1 |
分析 利用垂径定理的推论得出DO⊥AB,AF=BF,进而得出DF的长和△DEF∽△CEA,再利用相似三角形的性质求出即可.
解答 解:连接DO,交AB于点F,
∵D是$\widehat{AB}$的中点,
∴DO⊥AB,AF=BF,
∵AB=8,
∴AF=BF=4,
∴FO是△ABC的中位线,AC∥DO,
∵BC为直径,AB=8,AC=6,
∴BC=10,FO=$\frac{1}{2}$AC=3,
∴DO=5,
∴DF=5-3=2,
∵AC∥DO,
∴△DEF∽△CEA,
∴$\frac{CE}{DE}=\frac{AC}{FD}$,
∴$\frac{CE}{DE}=\frac{6}{2}$=3.
故选:D.
点评 此题主要考查了垂径定理的推论以及相似三角形的判定与性质,根据已知得出△DEF∽△CEA是解题关键.

练习册系列答案
相关题目
17.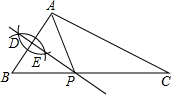 如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
 如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )
如图,已知△ABC中,AC<BC,分别以点A、点B为圆心,大于$\frac{1}{2}$AB长为半径作弧,两弧交于点D、点E;作直线DE交BC边于点P,连接AP.根据以上作图过程得出下列结论,其中不一定正确的是( )| A. | PA+PC=BC | B. | PA=PB | C. | DE⊥AB | D. | PA=PC |
14.下列说法正确的个数有( )
(1)两条直线被第三条直线所截,内错角相等
(2)如果∠1+∠2+∠3=180°,那么∠1、∠2、∠3互补
(3)对顶角相等
(4)如果两个角的两边分别平行,那么这两个角相等
(5)点到直线的垂线段叫做点到直线的距离.
(1)两条直线被第三条直线所截,内错角相等
(2)如果∠1+∠2+∠3=180°,那么∠1、∠2、∠3互补
(3)对顶角相等
(4)如果两个角的两边分别平行,那么这两个角相等
(5)点到直线的垂线段叫做点到直线的距离.
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
1.下列图形中既是轴对称又是中心对称的图形是( )
| A. |  | B. |  | C. |  | D. |  |
16.不等式组$\left\{\begin{array}{l}x-1>1\\ x+1≤4\end{array}\right.$的解集是( )
| A. | x<2 | B. | 2<x≤3 | C. | x≥3 | D. | 空集 |