题目内容
16.已知,点D为直线BC上一动点(点D不与点B、C重合),∠BAC=90°,AB=AC,∠DAE=90°,AD=AE,连接CE.(l)如图1,当点D在线段BC上时,求证:①BD⊥CE,②CE=BC-CD;
(2)如图2,当点D在线段BC的延长线上时,其他条件不变,请直接写出CE、BC、CD三条线段之间的关系;
(3)如图3,当点O在线段BC的反向延长线上时,且点A、E分别在直线BC的两侧,点F是DE的中点,连接AF、CF,其他条件不变,请判断△ACF的形状,并说明理由.
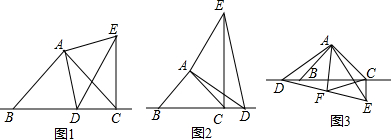
分析 (1)如图1中,只要证明△ABD≌△ACE,即可得到∠ABD=∠ACE=45°,BD=CE,由此可以证明.
(2)如图2中,结论:CE=BC+CD,证明方法类似(1).
(3)如图3中,结论:△ACF是等腰三角形,只要证明△ABD≌△ACE,即可得到∠ABD=∠ACE以及∠DCE=90°,再利用直角三角形斜边中线定理即可解决.
解答 (1)证明:如图1中,∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE,
∴∠ABD=∠ACE=45°,BD=CE,
∴∠ACB+∠ACE=90°
∴∠ECB=90°,
∴BD⊥CE,CE=BC-CD.
(2)如图2中,结论:CE=BC+CD,理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$,
∴△ABD≌△ACE,
∴BD=CE,
∴CE=BC+CD.
(3)如图3中,结论:△ACF是等腰三角形.理由如下:
∵∠BAC=∠DAE=90°,
∴∠BAD=∠CAE,
在△ABD和△ACE中,
$\left\{\begin{array}{l}{AB=AC}\\{∠BAD=∠CAE}\\{AD=AE}\end{array}\right.$
∴△ABD≌△ACE,
∴∠ABD=∠ACE,
∵∠ABC=∠ACB=45°,
∴∠ACE=∠ABD=135°,
∴∠DCE=90°,
又∵点F是DE中点,
∴AF=CF=$\frac{1}{2}$DE,
∴△ACF是等腰三角形.
点评 本题考查全等三角形的判定和性质、等腰三角形的判定和性质、直角三角形斜边中线定理等知识,解题的关键是正确寻找全等三角形,属于中考常考题型.

 精英口算卡系列答案
精英口算卡系列答案| 每天使用零花钱(单位:元) | 0 | 1 | 3 | 4 | 5 |
| 人数 | 1 | 3 | 5 | 4 | 2 |
| A. | 众数是5元 | B. | 极差是4元 | C. | 中位数3元 | D. | 平均数是2.5元 |
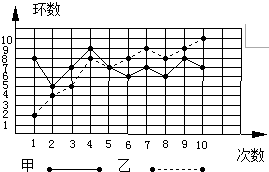
| A. | 甲、乙的总环数相等 | B. | 甲的成绩稳定 | ||
| C. | 甲、乙的众数相同 | D. | 乙的发展潜力更大 |
| A. | -π | B. | -3 | C. | -$\sqrt{5}$ | D. | 0 |
| A. | a2•a3=a6 | B. | a2+a3=a5 | C. | (a2)3=a6 | D. | (-2x)3=-6x3 |
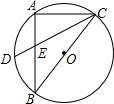 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )| A. | 7:2 | B. | 5:2 | C. | 4:1 | D. | 3:1 |
 在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上.DF=BE.求证:四边形BEDF是矩形.
在?ABCD中,过点D作DE⊥AB于点E,点F在边CD上.DF=BE.求证:四边形BEDF是矩形.

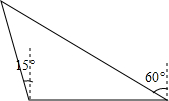 如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.