题目内容
15.社区敬老院需要600个环保包装盒,原计划由初三(1)班全体同学制作完成.但在实际制作时,有10名同学因为参加学校跳绳比赛而没有参加制作.这样,该班实际参加制作的同学人均制作的数量比原计划多5个,那么这个班级共有多少名同学?分析 设该班级共有x名同学,根据实际每个学生做的个数-原计划制作的个数=5,可列出关于x的分式方程,解方程即可得出结论.
解答 解:设该班级共有x名同学,
依题意得$\frac{600}{x-10}$-$\frac{600}{x}$=5,
解得:x=40,或x=-30(舍去).
检验:将x=40代入原方程,方程左边=20-15=5=右边,
故x=40是原方程的解.
答:这个班级共有40名同学.
点评 本题考查了分式方程的应用,解题的关键是根据数量关系列出关于x的分式方程.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程是关键.

练习册系列答案
相关题目
5.下列计算正确的是( )
| A. | a2•a3=a6 | B. | a2+a3=a5 | C. | (a2)3=a6 | D. | (-2x)3=-6x3 |
6.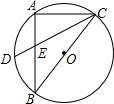 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )| A. | 7:2 | B. | 5:2 | C. | 4:1 | D. | 3:1 |
20.在一次夏令营活动中,小明同学从营地A出发,要到A地的北偏东60°方向的C处,他先沿正东方向走了200m到达B地,再沿B地北偏东30°方向走,恰好到达目的地C处,那么,由此可知,B,C两地相距为( )
| A. | 100m | B. | 150m | C. | 200m | D. | 250m |
4.在下列各式中,二次根式$\sqrt{a-1}$的有理化因式是( )
| A. | $\sqrt{a+1}$ | B. | $\sqrt{a-1}$ | C. | $\sqrt{a}+1$ | D. | $\sqrt{a}-1$ |
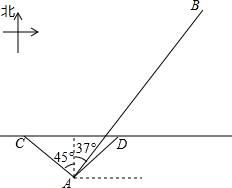 我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.
我国南海某海域有一个固定侦测点A,该侦测点的可侦测半径为$10\sqrt{2}$海里.某天,在点A侦测到西北方向上的点C处有一可疑船恰好进入侦测区域,且往正东方向匀速航行,我方与其进行多次无线电沟通无果后,可疑船只于2小时后恰好在D处离开侦测区域,我方立即通知(通知时间忽略不计)位于点A北偏东37°方向,且与A相距50海里的B处的军舰往正南方向对可疑船只进行侦测拦截.