题目内容
11.已知抛物线C:y=x2-4x+3.(1)求该抛物线关于y轴对称的抛物线C1的解析式.
(2)将抛物线C平移至C2,使其经过点(1,4).若顶点在x轴上,求C2的解析式.
分析 (1)利用原抛物线上的关于y轴对称的点的特点:纵坐标相同,横坐标互为相反数就可以解答.
(2)设平移后的解析式为:y=(x-h)2,代入点(1,4)求得h的值即可.
解答 解:(1)配方,y=x2-4x+3=(x-2)2-1.
∴抛物线C:顶点(2,-1),与y 轴交点(0,3)
∵C1与C关于y轴对称,
∴C1顶点坐标是(-2,-1),且与y轴交点(0,3).
设C1的解析式为y=a(x+2)2-1、把(0,3)代入,解得:a=1,
∴C1的解析式为y=x2+4x+3.
(2)由题意,可设平移后的解析式为:y=(x-h)2,
∵抛物线C2经过点(1,4),
∴(1-h)2=4,解得:h=-1或h=3,
∴C2的解析式为:y=(x+1)2或y=(x-3)2,
即y=x2+2x+1或y=x2-6x+9.
点评 本题考查了二次函数的图象与几何变换,解决本题的关键是抓住关于y轴对称的坐标特点和平移的规律.

练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
19.某商场为了促销,凡购买1000元商品的顾客获抽奖券一张.抽奖活动设置了如下的电翻奖牌,一张抽奖券只能有一次机会在9个数字中选中一个翻牌,其对应的反面就是奖品(重新启动会自动随机交换位置).
(1)求一张抽奖券翻到一台电风扇的概率;
(2)有两张抽奖券翻奖牌,请你根据题意写出一个事件,使这个事件发生的概率是$\frac{1}{9}$.
翻奖牌正面
翻奖牌反面.
(1)求一张抽奖券翻到一台电风扇的概率;
(2)有两张抽奖券翻奖牌,请你根据题意写出一个事件,使这个事件发生的概率是$\frac{1}{9}$.
| 1 | 2 | 3 |
| 4 | 5 | 6 |
| 7 | 8 | 9 |
| 一台电风扇 | 一台收音机 | 谢谢参与 |
| 谢谢参与 | 一副球拍 | 一个U盘 |
| 两张电影票 | 谢谢参与 | 一副球拍 |
6.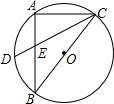 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
 如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )
如图,Rt△ABC内接于⊙O,BC为直径,AB=8,AC=6,D是弧AB的中点,CD与AB的交点为E,则CE:DE等于( )| A. | 7:2 | B. | 5:2 | C. | 4:1 | D. | 3:1 |
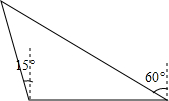 如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.
如图,A,B,C分别表示三所不同的学校,B,C在东西向的一条马路边,A学校在B学校北偏西15°方向上,在C学校北偏西60°方向上,A,B两学校之间的距离是1000米,请求出∠BAC的度数以及A,C两学校之间的距离.
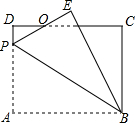 如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD=1,则AP的长为3.6.
如图,矩形ABCD中,AB=8,BC=6,P为AD上一点,将△ABP沿BP翻折至△EBP,PE与CD相交于点O,且OE=OD=1,则AP的长为3.6.