Question

14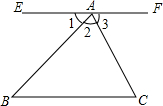．已知：如图，直线EF过点A，且EF∥BC，求证：∠BAC+∠B+∠C=180°．
证明：∵EF∥BC已知
∴∠1=∠B两直线平行，内错角相等
∠3=∠C两直线平行，内错角相等
∵∠1+∠2+∠3=180°平角的定义
∴∠BAC+∠B+∠C=180°等量代换．

Answer 1

分析 先根据平行线的性质得出∠1=∠B，∠3=∠C，再由补角的定义得出∠1+∠2+∠3=180°，利用等量代换即可得出结论．

解答 解：：∵EF∥BC（已知），
∴∠1=∠B（两直线平行，内错角相等），
∠3=∠C（两直线平行，内错角相等）．
∵∠1+∠2+∠3=180°（平角的定义），
∴∠BAC+∠B+∠C=180°（等量代换）．
故答案为：已知，两直线平行，内错角相等；两直线平行，内错角相等；平角的定义；等量代换．

点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，内错角相等．