题目内容
5. 如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.
如图,等腰三角形ABC中,AC=BC=10,AB=12,以BC为直径作⊙O交AB于点D,交AC于点G,DF⊥AC,垂足为F,交CB的延长线于点E.(1)求证:直线EF是⊙O的切线;
(2)求cos∠E的值.
分析 (1)求证直线EF是⊙O的切线,只要连接OD证明OD⊥EF即可;
(2)根据∠E=∠CBG,可以把求cos∠E的值得问题转化为求cos∠CBG,进而转化为求Rt△BCG中,两边的比的问题.
解答 (1)证明:如图,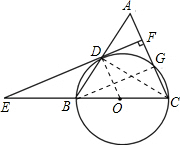
方法1:连接OD、CD.
∵BC是直径,
∴CD⊥AB.
∵AC=BC.
∴D是AB的中点.
∵O为CB的中点,
∴OD∥AC.
∵DF⊥AC,
∴OD⊥EF.
∴EF是圆O的切线.
方法2:∵AC=BC,
∴∠A=∠ABC,
∵OB=OD,
∴∠DBO=∠BDO,
∵∠A+∠ADF=90°
∴∠EDB+∠BDO=∠A+∠ADF=90°.
即∠EDO=90°,
∴OD⊥ED
∴EF是圆O的切线.
(2)解:连BG.
∵BC是直径,
∴∠BDC=90°.
∴CD=$\sqrt{A{C}^{2}-A{D}^{2}}$=8.
∵AB•CD=2S△ABC=AC•BG,
∴BG=$\frac{AB•CD}{AC}$=$\frac{96}{10}$=$\frac{48}{5}$.
∴CG=$\sqrt{B{C}^{2}-B{G}^{2}}$=$\frac{14}{5}$.
∵BG⊥AC,DF⊥AC,
∴BG∥EF.
∴∠E=∠CBG,
∴cos∠E=cos∠CBG=$\frac{BG}{BC}$=$\frac{24}{25}$.
点评 本题考查的是切线的判定,要证某线是圆的切线,已知此线过圆上某点,连接圆心和这点(即为半径),再证垂直即可.

练习册系列答案
 提分百分百检测卷单元期末测试卷系列答案
提分百分百检测卷单元期末测试卷系列答案
相关题目
16.若m=$\frac{\sqrt{2}}{2}$×(-2),则有( )
| A. | 0<m<1 | B. | -1<m<0 | C. | -2<m<-1 | D. | -3<m<-2 |
10.据有关资料显示,2014年通过国家科技支撑计划,遵义市获得国家级科技专项重点项目资金5533万元,将5533万用科学记数法可表示为( )
| A. | 5.533×108 | B. | 5.533×107 | C. | 5.533×106 | D. | 55.33×106 |
14.下列等式恒成立的是( )
| A. | (a+b)2=a2+b2 | B. | (ab)2=a2b2 | C. | a4+a2=a6 | D. | a2+a2=a4 |
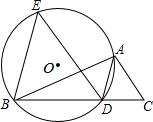 如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED
如图,已知AD是△ABC的角平分线,⊙O经过A、B、D三点.过点B作BE∥AD,交⊙O于点E,连接ED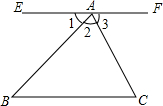 已知:如图,直线EF过点A,且EF∥BC,求证:∠BAC+∠B+∠C=180°.
已知:如图,直线EF过点A,且EF∥BC,求证:∠BAC+∠B+∠C=180°.