题目内容
1.如图,在一张长方形纸条上画一条数轴.
(1)若折叠纸条,数轴上表示-3的点与表示1的点重合,则折痕与数轴的交点表示的数为-1;
(2)若经过某次折叠后,该数轴上的两个数a和b表示的点恰好重合,则折痕与数轴的交点表示的数为$\frac{a+b}{2}$(用含a,b的代数式表示);
(3)若将此纸条沿虚线处剪开,将中间的一段纸条对折,使其左右两端重合,这样连续对折n次后,再将其展开,请分别求出最左端的折痕和最右端的折痕与数轴的交点表示的数.(用含n的代数式表示)
分析 (1)找出5表示的点与-3表示的点组成线段的中点表示数,然后结合数轴即可求得答案;
(2)先找出a表示的点与b表示的点所组成线段的中点,从而可求得答案;
(3)先求出每两条相邻折痕的距离,进一步得到最左端的折痕和最右端的折痕与数轴的交点表示的数,即可求得答案.
解答 解:(1)(-3+1)÷2
=-2÷2
=-1.
故折痕与数轴的交点表示的数为-1;
(2)折痕与数轴的交点表示的数为$\frac{a+b}{2}$(用含a,b的代数式表示);
(3)∵对折n次后,每两条相邻折痕的距离为$\frac{5-(-3)}{{2}^{n}}$=$\frac{8}{{2}^{n}}$,
∴最左端的折痕与数轴的交点表示的数是-3+$\frac{8}{{2}^{n}}$,最右端的折痕与数轴的交点表示的数是5-$\frac{8}{{2}^{n}}$.
故答案为:-1;$\frac{a+b}{2}$.
点评 本题主要考查的是数轴的认识,找出对称中心是解题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
9.已知等腰三角形的两边长分别为5和9,则该等腰三角形的周长为( )
| A. | 19 | B. | 23 | C. | 20或23 | D. | 19或23 |
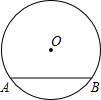 如图半径为6的⊙O中,弦AB=8,则圆心O到AB的距离为2$\sqrt{5}$.
如图半径为6的⊙O中,弦AB=8,则圆心O到AB的距离为2$\sqrt{5}$.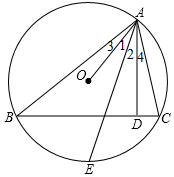 △ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).
△ABC的三个顶点在⊙O上,AD⊥BC,D为垂足,E是$\widehat{BC}$的中点,求证:∠1=∠2(提示:可以延长AO交⊙O于F,连接BF).