题目内容
6.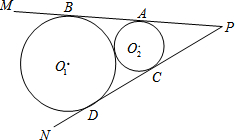 如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.
如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.(1)求AB的长?
(2)求PB+PC的值?
分析 (1)如图1,连接O1O2,O1B,O2A,过O2作O2E⊥BO1于E,由PM切⊙O1,⊙O2于B,A,得到O1B⊥AB,O2A⊥AB,于是求得四边形ABEO2是矩形,推出AB=O2E,BE=AO2=4,然后根据勾股定理即可得到结果;
(2)如图2,连接PO1,O1B,O2A,由于PM,PN切⊙O1,⊙O2于B,A,D,C,得到O1B⊥AB,O2A⊥AB,PA=PC,求得O1B∥AO2,推出△PAO2∽△PBO1,列出比例式即可得到结论.
解答 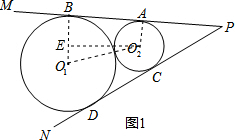 解:(1)如图1,连接O1O2,O1B,O2A,过O2作O2E⊥BO1于E,
解:(1)如图1,连接O1O2,O1B,O2A,过O2作O2E⊥BO1于E,
∵PM切⊙O1,⊙O2于B,A,
∴O1B⊥AB,O2A⊥AB,
∴四边形ABEO2是矩形,
∴AB=O2E,BE=AO2=4,
∴EO1=9-4=5,
∵⊙O1和⊙O2外切,
∴O1O2=9+4=13,
∴O2E2=O1O22-O1E2,
∴O1E=12,
∴AB=12;
(2)如图2,连接PO1,O1B,O2A,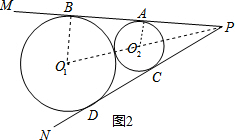
∵PM,PN切⊙O1,⊙O2于B,A,D,C,
∴O1B⊥AB,O2A⊥AB,PA=PC,
∴P,O1,O2在同一条直线上,O1B∥AO2,
∴△PAO2∽△PBO1,
∴$\frac{PA}{PB}=\frac{A{O}_{2}}{B{O}_{1}}$,
即$\frac{PA}{PA+12}=\frac{4}{9}$,
∴PA=$\frac{48}{5}$,
∴PC=$\frac{48}{5}$,PB=$\frac{48}{5}$+12=$\frac{108}{5}$,
∴PB+PC=$\frac{48}{5}$+$\frac{108}{5}$=$\frac{156}{5}$.
点评 本题考查了切线的性质,相切两圆的性质,相似三角形的判定和性质,矩形的性质,正确的作出辅助线是解题的关键.

 快乐5加2金卷系列答案
快乐5加2金卷系列答案| A. | a2+a=a3 | B. | (a3)2=a5 | C. | $\sqrt{3}$×$\sqrt{3}$=3 | D. | $\sqrt{16}$-$\sqrt{9}$=$\sqrt{7}$ |
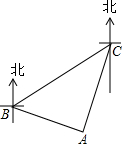 如图,某轮船航行至点A时,测得:轮船在小岛B的南偏东75°的方向,在航海塔C的南偏西20°,又知航海塔C在小岛B的北偏东65°的方向,下列结论正确的是( )
如图,某轮船航行至点A时,测得:轮船在小岛B的南偏东75°的方向,在航海塔C的南偏西20°,又知航海塔C在小岛B的北偏东65°的方向,下列结论正确的是( )| A. | ∠ABC=50° | B. | ∠BCA=55° | C. | ∠BAC=95° | D. | 以上都正确 |