题目内容
17.在△ABC中,若∠A=∠C=$\frac{1}{2}$∠B,这个三角形是直角三角形.分析 根据已知和三角形内角和定理求出$\frac{1}{2}$∠B+$\frac{1}{2}$∠B+∠B=180°,求出∠B=90°,即可得出答案.
解答 解:∵在△ABC中,若∠A=∠C=$\frac{1}{2}$∠B,∠A+∠B+∠C=180°,
∴$\frac{1}{2}$∠B+$\frac{1}{2}$∠B+∠B=180°,
∴∠B=90°,
∴△ABC是直角三角形.
故答案为:直角三角形.
点评 本题考查了三角形的内角和定理的应用,直角三角形的判定,注意:三角形的内角和等于180°.

练习册系列答案
相关题目
8.已知a-b=3,c+d=2,则(b+c)-(a-d)的值为( )
| A. | 1 | B. | -1 | C. | -5 | D. | 5 |
5.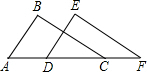 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )| A. | ∠A=∠EDF | B. | ∠B=∠E | C. | ∠BCA=∠F | D. | BC∥EF |
12.下列化简结果正确的是( )
| A. | $\sqrt{72}=6\sqrt{2}$ | B. | $(\sqrt{6a})^{2}=\sqrt{6}a$ | C. | $\sqrt{48}=2\sqrt{12}$ | D. | $\sqrt{20}=4\sqrt{5}$ |
2.若抛物线y=ax2经过P(1,-2),则它也经过( )
| A. | (2,1) | B. | (-1,2) | C. | (1,2) | D. | (-1,-2) |
7.如图,四个图形中的∠1和∠2,不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
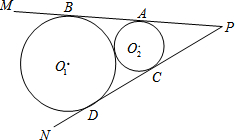 如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.
如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.