题目内容
1．若关于x的二次函数$y=（m+2）{x^{{m^2}+m-4}}-m+6$是关于x的二次函数，且其图象顶点为最高点，则顶点的坐标为（0，9）．分析 根据二次函数的定义列出关于m的方程和不等式，求出m的值，根据二次函数的性质求出顶点坐标．
解答 解：由题意得，m2+m-4=2，m+2＜0，
解方程m2+m-4=2得，m=-3或2，
解不等式m+2＜0得m＜-2，
则m=-3，
函数解析式为y=-x2+9，
则顶点的坐标为（0，9）．
故答案为：（0，9）．
点评 本题考查的是二次函数的定义和二次函数的性质，掌握形如y=ax2+bx+c（a≠0）的式子为二次函数和二次函数的性质是解题的关键．
练习册系列答案
相关题目
12．下列化简结果正确的是（ ）
| A． | $\sqrt{72}=6\sqrt{2}$ | B． | $（\sqrt{6a}）^{2}=\sqrt{6}a$ | C． | $\sqrt{48}=2\sqrt{12}$ | D． | $\sqrt{20}=4\sqrt{5}$ |
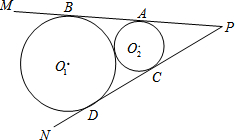如图，已知半径是9的⊙O1和半径是4的⊙O2外切，过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D．
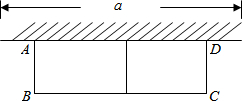已知：如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S米2．