题目内容
15.当x≤2时,$\sqrt{2-x}$在实数范围内有意义;当x≠4时,分式$\frac{1}{x-4}$有意义.分析 根据二次根式有意义的条件可得2-x≥0,解不等式即可;根据分式有意义的条件可得x-4≠0,再解即可.
解答 解:∵$\sqrt{2-x}$在实数范围内有意义,
∴2-x≥0,
解得:x≤2;
∵分式$\frac{1}{x-4}$有意义,
∴x-4≠0,
解得:x≠4,
故答案为:≤2;≠4.
点评 此题主要考查了二次根式有意义和分式有意义的条件,关键是掌握分式有意义,分母不为0;二次根式的被开方数是非负数.

练习册系列答案
 心算口算巧算一课一练系列答案
心算口算巧算一课一练系列答案
相关题目
5.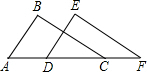 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
 如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )
如图,已知点A、D、C、F在同一直线上,且AB=DE,BC=EF,要使△ABC≌△DEF,还需要添加的一个条件是( )| A. | ∠A=∠EDF | B. | ∠B=∠E | C. | ∠BCA=∠F | D. | BC∥EF |
7.如图,四个图形中的∠1和∠2,不是同位角的是( )
| A. |  | B. |  | C. |  | D. |  |
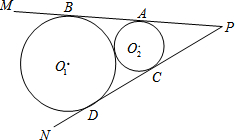 如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.
如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.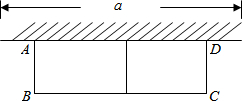 已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2.
已知:如图,有长为24米的篱笆,一面利用墙(墙的最大可用长度a为10米),围成中间隔有一道篱笆的长方形花圃.设花圃的宽AB为x米,面积为S米2. 如图是由七块形状相同的正方体积木搭成的几何体,请画出从正面、左面和上面看到的这个几何体的形状图.
如图是由七块形状相同的正方体积木搭成的几何体,请画出从正面、左面和上面看到的这个几何体的形状图.