题目内容
11.下列计算正确的是( )| A. | a2+a=a3 | B. | (a3)2=a5 | C. | $\sqrt{3}$×$\sqrt{3}$=3 | D. | $\sqrt{16}$-$\sqrt{9}$=$\sqrt{7}$ |
分析 直接利用二次根式的乘法运算法则以及幂的乘方和合并同类项法则化简求出即可.
解答 解:A、a2+a,无法计算,故此选项错误;
B、(a3)2=a6,故此选项错误;
C、$\sqrt{3}$×$\sqrt{3}$=3,正确;
D、$\sqrt{16}$-$\sqrt{9}$=4-3=1,故此选项错误;
故选:C.
点评 此题主要考查了二次根式的乘法运算以及幂的乘方和合并同类项,正确掌握运算法则是解题关键.

练习册系列答案
相关题目
1.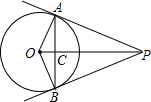 如图,已知PA,PB切⊙O于A,B两点,OP交AB于点C,则图中能用字母表示的直角三角形共有( )
如图,已知PA,PB切⊙O于A,B两点,OP交AB于点C,则图中能用字母表示的直角三角形共有( )
 如图,已知PA,PB切⊙O于A,B两点,OP交AB于点C,则图中能用字母表示的直角三角形共有( )
如图,已知PA,PB切⊙O于A,B两点,OP交AB于点C,则图中能用字母表示的直角三角形共有( )| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
2.若抛物线y=ax2经过P(1,-2),则它也经过( )
| A. | (2,1) | B. | (-1,2) | C. | (1,2) | D. | (-1,-2) |
19. 如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
 如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )
如图一个矩形减去一个以宽为边长的正方形后,所剩下的矩形与原矩形相似,则原矩形的长与宽的比值为( )| A. | $\frac{{3+\sqrt{5}}}{2}$ | B. | $\frac{{\sqrt{5}-1}}{2}$ | C. | $\frac{{3-\sqrt{5}}}{2}$ | D. | $\frac{{\sqrt{5}+1}}{2}$ |
16.已知x1=5,x2=-5是一元二次方程x2+ax+b=0的两个根,则a,b的值为( )
| A. | a=25,b=-25 | B. | a=0,b=-25 | C. | a=25,b=25 | D. | a=0,b=25 |
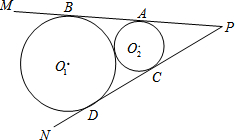 如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.
如图,已知半径是9的⊙O1和半径是4的⊙O2外切,过P点同时作⊙O1和⊙O2的切线PM、PN切点分别是A、B、C、D.