等腰三角形两边长分别为4.7.则其周长等于15或18．题目和参考答案——青夏教育精英家教网——

题目内容

18．等腰三角形两边长分别为4、7，则其周长等于15或18．

分析本题没有明确说明已知的边长哪个是腰长，则有两种情况：①腰长为4；②腰长为7．再根据三角形的性质：三角形的任意两边的和＞第三边，任意两边之差＜第三边判断是否满足，再将满足的代入周长公式即可得出周长的值．

解答解：①腰长为4时，符合三角形三边关系，则其周长=4+4+7=15；
②腰长为7时，符合三角形三边关系，则其周长=7+7+4=18．
所以三角形的周长为15或18．
故答案为：15或18．

点评本题考查了等腰三角形的性质和三角形的三边关系；已知没有明确腰和底边的题目一定要想到两种情况，分类进行讨论，还应验证各种情况是否能构成三角形进行解答，这点非常重要，也是解题的关键．

练习册系列答案

导学精析与训练系列答案

红果子三级测试卷系列答案

悦然好学生单元练系列答案

实验班提优课堂系列答案

英才考评系列答案

课堂练加测系列答案

百分百训练系列答案

新体验课时训练系列答案

尖子班系列答案

高分拔尖课时作业系列答案

相关题目

8．已知a-b=3，c+d=2，则（b+c）-（a-d）的值为（　　）

9．计算：（$\frac{1}{3}$）^-2-4tan45°-$\sqrt{（-2）^{2}}$+|3-π|

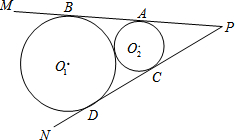如图，已知半径是9的⊙O₁和半径是4的⊙O₂外切，过P点同时作⊙O₁和⊙O₂的切线PM、PN切点分别是A、B、C、D．
（1）求AB的长？
（2）求PB+PC的值？

13．某公司销售一种新型节能产品，现准备从国内和国外两种销售方案中选择一种进行销售．若只在国内销售，销售价格y（元/件）与月销量x（件）的函数关系式为y=-$\frac{1}{100}$x+150，成本为20元/件，无论销售多少，每月还需支出广告费62500元，设月利润为w_内（元）（利润=销售额-成本-广告费）．若只在国外销售，销售价格为150元/件，受各种不确定因素影响，成本为a元/件（a为常数，10≤a≤40），当月销量为x（件）时，每月还需缴纳$\frac{1}{100}$x² 元的附加费，设月利润为w_外（元）（利润=销售额-成本-附加费）．
（1）当x=1000时，y=140元/件，w_内=57500元；
（2）分别求出w_内，w_外与x间的函数关系式（不必写x的取值范围）；
（3）当x为何值时，在国内销售的月利润最大？若在国外销售月利润的最大值与在国内销售月利润的最大值相同，求a的值；
（4）如果某月要将5000件产品全部销售完，请你通过分析帮公司决策，选择在国内还是在国外销售才能使所获月利润较大？

3．（$\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$）÷$\frac{x+2}{{x}^{2}-2x+1}$，先化简，再请你为x任选一个适当的数代入求值．

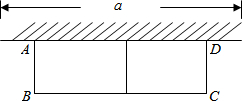已知：如图，有长为24米的篱笆，一面利用墙（墙的最大可用长度a为10米），围成中间隔有一道篱笆的长方形花圃．设花圃的宽AB为x米，面积为S米²．
（1）求S与x的函数关系式及自变量的取值范围；
（2）如果要围成面积为45米²的花圃，AB的长是多少米？

7．如图，四个图形中的∠1和∠2，不是同位角的是（　　）

8．若一个正六边形的周长为24，则该正六边形的面积为（　　）