题目内容
13.“十一”期间,小明和父母一起开车到距家200千米的景点旅游,出发前,汽车油箱内储油45升,当行驶150千米时,发现油箱油箱余油量为30升(假设行驶过程中汽车的耗油量是均匀的).(1)求该车平均每千米的耗油量,并写出行驶路程x(千米)与剩余油盘Q(升)的关系式;
(2)当x=280(千米)时,求剩余油量Q的值;
(3)当油箱中剩余油盘低于3升时,汽车将自动报警,如果往返途中不加油,他们能否在汽车报警前回到家?请说明理由.
分析 (1)根据平均每千米的耗油量=总耗油量÷行驶路程即可得出该车平均每千米的耗油量,再根据剩余油量=总油量-平均每千米的耗油量×行驶路程即可得出Q关于x的函数关系式;
(2)代入x=280求出Q值即可;
(3)根据行驶的路程=耗油量÷平均每千米的耗油量即可求出报警前能行驶的路程,与景点的往返路程比较后即可得出结论.
解答 解:(1)该车平均每千米的耗油量为(45-30)÷150=0.1(升/千米),
行驶路程x(千米)与剩余油盘Q(升)的关系式为Q=45-0.1x;
(2)当x=280时,Q=45-0.1×280=17(L).
答:当x=280(千米)时,剩余油量Q的值为17L.
(3)(45-3)÷0.1=420(千米),
∵420>400,
∴他们能在汽车报警前回到家.
点评 本题考查了函数的关系式以及一次函数图象上点的坐标特征,根据数量关系列出函数关系式是解题的关键.

练习册系列答案
 小学生10分钟口算测试100分系列答案
小学生10分钟口算测试100分系列答案
相关题目
3.若a、b都是不为零的数,则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|ab|}{ab}$的结果为( )
| A. | 3或-3 | B. | 3或-1 | C. | -3或1 | D. | 3或-1或1 |
18.已知反比例函数y=$\frac{k}{x}$(k≠0)的图象在其所在现象内,y的值随x的值的增大而增大,则反比例函数y=$\frac{k}{x}$的图象在( )
| A. | 第一、二象限 | B. | 第一、三象限 | C. | 第二、三象限 | D. | 第二、四象限 |
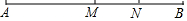 如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )
如图所示,点M,N是线段AB上的两个点,且M是AB的中点,N是MB的中点,若AB=a,NB=b,下列结论:①AM=$\frac{1}{2}$a②AN=a-b③MN=$\frac{1}{2}$a-b④MN=$\frac{1}{4}$a.其中正确的有( )