题目内容
3.若a、b都是不为零的数,则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|ab|}{ab}$的结果为( )| A. | 3或-3 | B. | 3或-1 | C. | -3或1 | D. | 3或-1或1 |
分析 可从a、b同号,a、b异号,分类讨论得出结论.
解答 解:①当a>0,b>0时
则$\frac{|a|}{a}$+$\frac{|b|}{b}$+$\frac{|ab|}{ab}$
=1+1=3;
②当a<0,b<0时
$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|ab|}{ab}$
=-1-1+1
=-1;
③当a>0,b<0时
$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|ab|}{ab}$
=1-1-1
=-1;
④当a<0,b>0时
$\frac{|a|}{a}+\frac{|b|}{b}+\frac{|ab|}{ab}$
=-1+1-1
=-1;
故选B.
点评 本题考查了绝对值的意义及分式的化简.正数和0的绝对值是它本身,负数和0的绝对值是它的相反数.互为相反数(0除外)的两个数的商为1,相同两个数(0除外)的商为1.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
13.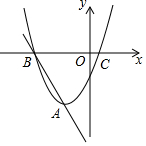 已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
(1)求直线AB的解析式;
(2)当y1<y2时,根据图象直接写出自变量x的取值范围.
 已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.
已知抛物线y1=x2+2x-3的顶点为A,与x轴交于点B、C(B在C的左边),直线y2=kx+b过A、B两点.(1)求直线AB的解析式;
(2)当y1<y2时,根据图象直接写出自变量x的取值范围.
18.下列事件中,属于必然事件的是( )
| A. | 在只装了红球的袋子中摸到白球 | |
| B. | 某射击运动员射击一次,命中靶心 | |
| C. | 任意画一个三角形,其内角和是180° | |
| D. | 掷一枚质地均匀的正方体骰子,向上的一面点数是3 |
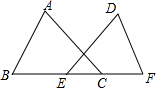 如图,点E,C在BF上,BE=CF,AB=DF,∠B=∠F.求证:∠A=∠D.
如图,点E,C在BF上,BE=CF,AB=DF,∠B=∠F.求证:∠A=∠D.